Pontrendszerek - 3.1.11
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 13., 13:30-kor történt szerkesztése után volt.
Feladat
- Az
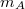 tömegű
tömegű  és az
és az 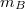 tömegű
tömegű  szabad anyagi pontok Newton törvénye szerint kölcsönösen vonzzák egymást. A kezdő időpontban az
szabad anyagi pontok Newton törvénye szerint kölcsönösen vonzzák egymást. A kezdő időpontban az  pont sebessége
pont sebessége 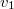 és
és 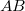 -re merőleges,
-re merőleges,  pont sebessége
pont sebessége 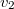 ,
, 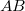 irányú és
irányú és  -tól elfelé mutat. Határozzuk meg a pontok súlypontjának pályáját és sebességét!
-tól elfelé mutat. Határozzuk meg a pontok súlypontjának pályáját és sebességét!
Megoldás
- Vegyük fel a kétdimenziós vonatkoztatási rendszert úgy, hogy az
 pont az origóban van és a
pont az origóban van és a  az
az  -tengely pozitív felére illeszkedik. Ekkor a pontok sebessége a kezdeti időpillanatban a tömegközéppont sebessége pedig
-tengely pozitív felére illeszkedik. Ekkor a pontok sebessége a kezdeti időpillanatban a tömegközéppont sebessége pedig![\[\mathbf{v}_{A}=\left[\begin{array}{c} v_{1} \\ 0\end{array}\right]\qquad\qquad \mathbf{v}_{B}=\left[\begin{array}{c} 0 \\ v_{2}\end{array}\right]\,,\]](/images/math/3/9/9/399c63f8185cc6518c1fc0f9d8fd129f.png) A két tömegpont alkotta pontrendszerre külső erők nem hatnak a mozgásuk során, ezért a teljes impulzus időben állandó. A teljes tömeg nem változik, azért ez egyúttal azt is jelenti, hogy a tömegközéppont sebessége is állandó. Tehát a fenti eredmény megadja a tömegközéppont sebességét a mozgás teljes idő tartama alatt.
A két tömegpont alkotta pontrendszerre külső erők nem hatnak a mozgásuk során, ezért a teljes impulzus időben állandó. A teljes tömeg nem változik, azért ez egyúttal azt is jelenti, hogy a tömegközéppont sebessége is állandó. Tehát a fenti eredmény megadja a tömegközéppont sebességét a mozgás teljes idő tartama alatt.![\[\mathbf{v}_{TKP}=\frac{m_{A}\mathbf{v}_{A}+m_{B}\mathbf{v}_{B}}{m_{A}+m_{B}}=\frac{1}{m_{A}+m_{B}}\left[\begin{array}{c} m_{A}v_{1} \\ m_{B}v_{2}\end{array}\right]\,.\]](/images/math/9/5/e/95eceb3f4293ce7b5320fbb41a0fe58d.png)
- Vegyük fel a kétdimenziós vonatkoztatási rendszert úgy, hogy az