Pontrendszerek - 3.1.16
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 13., 13:40-kor történt szerkesztése után volt.
Feladat
- Valamely
tömegű test rugalmatlanul ütközik egy 
tömegű testtel. Határozzuk meg hányadrésze vész el a kinetikus energiának, ha az tömegű test az ütközés előtt nyugalomban volt!
Megoldás
- Az ütközés során megmarad az impulzus és a tökéletes rugalmatlanság miatt az ütközés utáni sebességek megegyeznek. Ha az tömegű test ütközés előtti sebességét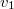
-gyel, az ütközés utáni sebességet pedig 
-vel jelöljük, akkor az impulzus megmaradást az alábbiak szerint írhatjuk fel. A kinetikus energia veszteség aránya![\[m_{1}v_{1}=(m_{1}+m_{2})v\qquad\Rightarrow\qquad v=\frac{m_{1}}{m_{1}+m_{2}}v_{1}\]](/images/math/1/c/4/1c4d9898b282950093079eabfee1eb9f.png)
![\[\frac{E_{kin,0}-E_{kin}}{E_{kin,0}}=\frac{\frac{1}{2}m_{1}v_{1}^{2}-\frac{1}{2}(m_{1}+m_{2})v^{2}}{\frac{1}{2}m_{1}v_{1}^{2}}=\frac{m_{2}}{m_{1}+m_{2}}\,.\]](/images/math/4/a/c/4acbbef7f6072086b353b70de4ca1e90.png)
- Az ütközés során megmarad az impulzus és a tökéletes rugalmatlanság miatt az ütközés utáni sebességek megegyeznek. Ha az
