Mechanika - Rezgések II.

Feladatok

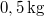1. (**6.30.) Egy $\setbox0\hbox{$0,5\,\rm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű testet olyan rugóra függesztünk, amely 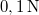$\setbox0\hbox{$0,1\,\rm N$}% \message{//depth:\the\dp0//}% \box0%$ erő hatására 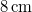$\setbox0\hbox{$8\,\rm{cm}$}% \message{//depth:\the\dp0//}% \box0%$-rel nyúlik meg. A testre mozgása során sebességével arányos ellenállás hat, amely 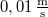$\setbox0\hbox{$0,01\,\rm{\frac ms}$}% \message{//depth:\the\dp0//}% \box0%$ sebesség esetén 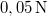$\setbox0\hbox{$0,05\,\rm N$}% \message{//depth:\the\dp0//}% \box0%$. 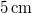A $\setbox0\hbox{$t=0$}% \message{//depth:\the\dp0//}% \box0%$ pillanatban a testet $\setbox0\hbox{$5\,\rm{cm}$}% \message{//depth:\the\dp0//}% \box0%$-rel kimozdítjuk egyensúlyi helyzetéből, és kezdősebesség nélkül indítjuk. Határozzuk meg a test mozgását!
   Útmutatás

   Állapítsuk meg, hogy a csillapított rezgés melyik alesetéről van szó, és vegyünk fel egy ahhoz illeszkdeő általános megoldást.
   Végeredmény

   $\[x(t)=e^{-5t}[0,0527\sinh(4,74t)+0,05\cosh(4,74t)],\]$

   ahol a számértékek SI alapegységben értendők.
   Megoldás
   
   
2. (6.31.) Hogyan változik meg az előző feladatban a test mozgása, ha olyan rugóra akasztjuk, amely 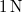$\setbox0\hbox{$1\,\rm N$}% \message{//depth:\the\dp0//}% \box0%$ hatására 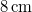$\setbox0\hbox{$8\,\rm{cm}$}% \message{//depth:\the\dp0//}% \box0%$-rel nyúlik meg és minden egyéb körülményt változatlanul hagyunk?
   Végeredmény

   $\[x(t)=e^{-5t}(0,05+0,25t),\]$

   ahol a számértékek SI alapegységekben értendők.
   Megoldás
   
   
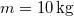3. (*6.32.) $\setbox0\hbox{$m=10\,\rm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű anyagi pont egy a centrumtól mért távolsággal arányos visszatérítő erő hatására egyenesvonalú lengéseket végez. A környező közeg ellenállása a pont sebességével arányos. Határozzuk meg a $\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$ rezgésidőt, ha az amplitúdó három teljes lengés után tizedére csökken! (A rugóállandó: $\setbox0\hbox{$D=20\,\rm{\frac Nm}$}% \message{//depth:\the\dp0//}% \box0%$)
   Útmutatás

   Vezessünk be egy időfüggő amplitúdót, és használjuk a csillapított frekvenciára vonatkozó összefüggést!
   Végeredmény

   $\[T=4,48\,\rm s\]$
   Megoldás
   
   
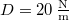4. (6.33.) Egy csillapított rezgésnél az amlitúdó hat teljes rezgés után tizedére csökken. A rezgésidő 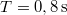$\setbox0\hbox{$T=0,8\,\rm s$}% \message{//depth:\the\dp0//}% \box0%$. Határozzuk meg a rezgési folyamatra jellemző D/m állandót és $\setbox0\hbox{$\beta$}% \message{//depth:\the\dp0//}% \box0%$ csillapítási tényezőt!
   Végeredmény

   $\[\beta=0,48\,\rm{\frac1s}\]$

   $\[\frac Dm=62\,\rm{\frac1{s^2}}\]$
   Megoldás
   
   
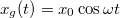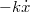5. (6.34.) $\setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0%$ direkciós erejű rugó felfüggesztési pontja $\setbox0\hbox{$x_g(t)=x_0\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%$ szerint mozog. A rugóra függesztett $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű test súrlódó közegbe nyúlik, ezért $\setbox0\hbox{$-k\dot x$}% \message{//depth:\the\dp0//}% \box0%$ fékező erő hat rá. Mekkora a test stacionárius rezgéseinek amplitúdója?
   Útmutatás

   A mozgásegyenletben a rugóerőben a megnyúlást módosítani kell, mivel azon keresztül jelenik meg a gerjesztés.
   Végeredmény

   $\[A(\omega)=\frac{\omega_0^2x_0}{\sqrt{(\omega_0^2-\omega^2)^2+(2\beta\omega)^2}}\]$
   Megoldás
   
   
6. (*6.35.) Csillapított lineáris harmonikus oszcillátort kényszerrezgésbe hozunk. A mozgás folyamán lesz olyan időpont, amikor az oszcillátor sebessége a legnagyobb. Ha megváltoztatjuk a kényszererő frekvenciáját, megváltozik a legnagyobb sebesség értéke is. Hogyan válasszuk meg a kényszerrezgés frekvenciáját, hogy ez a legnagyobb sebesség (mint a frekvencia függvénye) maximális legyen? Mekkora körfrekvenciánál legnagyobb a rezgés amplitúdója?
   Végeredmény

   $\[\omega=\omega_0\]$

   $\[\omega^2=\omega_0^2-2\beta^2\]$
   Megoldás
   
   
7. (**6.36.) Valamely csillapított, kényszerrezgést végző rendszer jósági tényezőjét a következőképpen definiáljuk:
   $\[Q=2\pi\frac{\text{a rendszer által tárolt energia}}{\text{egy periódus alatt disszipált energia}}\]$
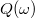   Határozzuk meg a $\setbox0\hbox{$Q(\omega)$}% \message{//depth:\the\dp0//}% \box0%$ függvényt!
   Útmutatás

   Határozzuk meg az átlagos mozgási és rugalmas energiát egy periódusra, valamint a gerjesztő erő teljesítményének integrálját szintén egy periódusra.
   Végeredmény

   $\[Q(\omega)=\frac{\omega_0^2+\omega^2}{4\omega\beta}\approx\frac{\omega_0}{2\beta}=\frac{\omega_0}{\Delta\omega_{1/2}}\]$

   a sebességrezonancia közelében.
   Megoldás