Mechanika - Jósági tényező
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. január 4., 00:35-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (**6.36.) Valamely csillapított, kényszerrezgést végző rendszer jósági tényezőjét a következőképpen definiáljuk: Határozzuk meg a
![\[Q=2\pi\frac{\text{a rendszer által tárolt energia}}{\text{egy periódus alatt disszipált energia}}\]](/images/math/2/6/7/2671604eec4fc02ad220a2603bb228ce.png)
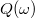 függvényt!
függvényt!
Megoldás
A rendszer által tárolt energia a kialakuló harmonikus rezgés energiája, amit az állandósult állapot állandó amplitúdója miatt könnyedén felírhatnánk az![\[E=\frac12DA(\omega)^2\]](/images/math/7/2/7/727f493ad481ee73760a5dd55ee7692d.png)
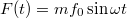 a gerjesztő erő. A kialakuló rezgés időfüggése
a gerjesztő erő. A kialakuló rezgés időfüggése 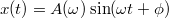 , a sebességé pedig
, a sebességé pedig ![\[v(t)=\omega A(\omega)\cos(\omega t+\phi)=\omega A(\omega)(\cos\omega t\cos\phi-\sin\omega t\sin\phi).\]](/images/math/a/a/5/aa52791f376ec13b0cd1b26998276c25.png)
![\[<E_m>=\frac12m<v^2(t)>=\frac12m\omega^2A(\omega)^2\frac12,\]](/images/math/8/2/8/828702bec975a553fa8d866ccc09ce2e.png)
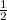 . Hasonlóan
. Hasonlóan ![\[<E_r>=\frac12D<x^2(t)>=\frac12m\omega_0^2A(\omega)^2\frac12.\]](/images/math/9/a/8/9a80b96d99cdfea04275523a397c0d06.png)
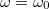 gerjesztési frekvenciánál egyenlő! A tárolt energia tehát:
gerjesztési frekvenciánál egyenlő! A tárolt energia tehát: ![\[E=\frac{\frac14mf_0^2(\omega_0^2+\omega^2)}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}\]](/images/math/7/d/1/7d1822b2f9146676dfc1f687c06b7b2b.png)
 periódus alatt, azaz
periódus alatt, azaz ![\[\Delta E=\int_0^TF(t)v(t)\rm dt\]](/images/math/4/9/4/4943e8e5974211401d512871317a82bc.png)
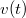 fenti második alakja miatt két tagból fog állni, és az időfüggetlen konstansokat kiemelve lényegében kétféle integrált kell meghatározni. Ebből az egyik:
fenti második alakja miatt két tagból fog állni, és az időfüggetlen konstansokat kiemelve lényegében kétféle integrált kell meghatározni. Ebből az egyik: ![\[\int_0^T\sin\omega t\cos\omega t\rm dt=0,\]](/images/math/6/4/9/649f6e14014e8a9a4880b8fc06b8ca73.png)
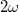 frekvenciájú szinuszfüggvény alatti előjeles területet jelent, ami két teljes
frekvenciájú szinuszfüggvény alatti előjeles területet jelent, ami két teljes 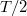 periódusára számolva éppen nulla. Marad tehát (a negatív előjeltől eltekintve)
periódusára számolva éppen nulla. Marad tehát (a negatív előjeltől eltekintve) ![\[\Delta E=mf_0\omega A(\omega)\sin\phi\int_0^T\sin^2\omega t\rm dt,\]](/images/math/2/3/d/23dc4a5901a96876730f524b347f8d0f.png)
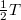 , azaz az átlagérték és az integrálási tartomány szorzata. A fázistolás szinusza
, azaz az átlagérték és az integrálási tartomány szorzata. A fázistolás szinusza 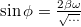 , mely gyök az amplitúdó
, mely gyök az amplitúdó 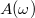 kifejezésében is látható. Összességében tehát
kifejezésében is látható. Összességében tehát ![\[\Delta E=mf_0\omega\frac{f_0}{\sqrt{...}}\frac T2\frac{2\beta\omega}{\sqrt{...}}=\frac{mf_0^2\omega^2T\beta}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}\]](/images/math/9/d/c/9dccf58dacf96b8f519adf244f117d1c.png)
![\[Q(\omega)=2\pi\frac{\frac14mf_0^2(\omega_0^2+\omega^2))}{mf_0^2\omega^2T\beta}=\frac{\omega_0^2+\omega^2}{4\omega\beta},\]](/images/math/0/f/2/0f26d020c08eff527fcebc5b8f90187b.png)
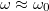 gerjesztés esetén
gerjesztés esetén ![\[Q\approx\frac{\omega_0}{2\beta}=\frac{\omega_0}{\Delta\omega_{1/2}}\]](/images/math/5/4/e/54e6f9b8bfc9819841efc7aa24ac13c1.png)