Mechanika - Csillapodó rezgés paraméterei
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. december 3., 14:35-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rezgések II. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (6.33.) Egy csillapított rezgésnél az amlitúdó hat teljes rezgés után tizedére csökken. A rezgésidő
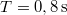 . Határozzuk meg a rezgési folyamatra jellemző D/m állandót és
. Határozzuk meg a rezgési folyamatra jellemző D/m állandót és  csillapítási tényezőt!
csillapítási tényezőt!
Megoldás
A csillapodásból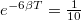 , azaz
, azaz ![\[\beta T=\frac{\ln(10)}6\]](/images/math/6/3/9/63957c3f01ac806f8a2328ba4ebc72e6.png)
![\[\beta=\frac{\ln(10)}{6T}=0,48\,\rm{\frac1s}\]](/images/math/e/e/8/ee832f830420065f0d9f5b02098a88ad.png)
![\[\frac Dm=\omega_0^2=\omega^2+\beta^2=(\frac{2\pi}T)^2+\beta^2=62\,\rm{\frac1{s^2}}\]](/images/math/8/f/9/8f9055a81fd84aa8c3c2de82dd0cc910.png)