Mechanika - Merev testek I.
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Werner (vitalap | szerkesztései) 2014. október 29., 11:58-kor történt szerkesztése után volt.
Feladatok
- (3.2.1.) Merev test egyenletesen gyorsuló forgó mozgást végez. Szögsebessége
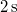 alatt
alatt 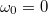 -ról
-ról 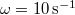 -ra változik. Mekkora a szöggyorsulása? Mekkora a szögelfordulása
-ra változik. Mekkora a szöggyorsulása? Mekkora a szögelfordulása 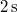 alatt? Mekkora a kerületi gyorsulása a tengelytől
alatt? Mekkora a kerületi gyorsulása a tengelytől 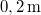 távolságra levő tömegpontnak?
távolságra levő tömegpontnak?
- (3.2.2.) Mekkora forgatónyomaték hat arra a
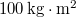 tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva
tehetetlenségi nyomatékú testre, amely nyugalomból indulva a forgatónyomaték hatására egyenletesen gyorsulva 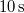 alatt 50 fordulatot tesz meg?
alatt 50 fordulatot tesz meg?
- (3.2.3.) Egy
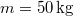 és
és 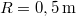 sugarú homogén lendítőkerék
sugarú homogén lendítőkerék 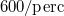 fordulatszámmal forog. A korong pereme és a féktuskó között a súrlódási együttható 0,5.
fordulatszámmal forog. A korong pereme és a féktuskó között a súrlódási együttható 0,5.
- a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az
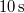 alatt megálljon?
alatt megálljon?
- b) Mekkora a megállítás ideje alatt a súrlódó erő munkája?
- a) Mekkora erővel kell a féktuskót a koronghoz szorítani, hogy az
- (*3.2.4.)
 sugarú
sugarú  tömegű gömböt egy, sugarának gömbfelület menti végpontján átmenő tengely körül megforgatunk.
tömegű gömböt egy, sugarának gömbfelület menti végpontján átmenő tengely körül megforgatunk.
- a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan
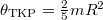 ?
?
- b) Mekkora nyomatékra van szükség ahhoz, hogy
 nagyságú szöggyorsulással tudjuk forgásba hozni?
nagyságú szöggyorsulással tudjuk forgásba hozni?
- c) Hogyan kell változni az idő függvényében azon energiaforrás teljesítményének, amely az állandó
 szöggyorsulást biztosítani képes, ha a gömb a
szöggyorsulást biztosítani képes, ha a gömb a  időpontban nyugalomból indult?
időpontban nyugalomból indult?
- a) Mekkora a gömb adott tengelyre vonatkozó tehetetlenségi nyomatéka, ha súlyponti tengelyére vonatkozóan
- (*3.2.5.) Rögzített tengely körül forgó
 tömegű és
tömegű és  sugarú korong kerületére fonalat csavarunk. A fonalat állandó
sugarú korong kerületére fonalat csavarunk. A fonalat állandó  teljesítményű energiaforrással kapcsolatban álló szerkezet feszíti.
teljesítményű energiaforrással kapcsolatban álló szerkezet feszíti.
- a) Hogyan változik a korong szöggyorsulása az idő függvényében, ha a korong a
 időpontban nyugalomban volt?
időpontban nyugalomban volt?
- b) Mennyi ideig kell a fonalat húzni, ha a korong forgási energiáját
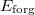 értékre akarjuk növelni?
értékre akarjuk növelni?
- a) Hogyan változik a korong szöggyorsulása az idő függvényében, ha a korong a
- (*3.2.6.) Mekkora egy
 hosszúságú pálca lengésideje, ha a felső végétől
hosszúságú pálca lengésideje, ha a felső végétől 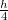 távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?
távolságra levő pontján átmenő tengely körül leng kis szögkitéréssel?
- (*3.2.7.) Egy
 tömegű
tömegű  sugarú, homogén tömegeloszlású korong egy kerületi pontján átmenő tengely körül kis szögkitérésű lengéseket végez. A forgástengely a korong homloklapjára merőleges.
sugarú, homogén tömegeloszlású korong egy kerületi pontján átmenő tengely körül kis szögkitérésű lengéseket végez. A forgástengely a korong homloklapjára merőleges.
- a) Írd fel a korong mozgásegyenletét, mikor az egyensúlyi helyzetéből kimozdult helyzetben van!
- b) Mekkora a korong lengésének periódusideje?
- (**3.2.10.) Egy
 és
és  oldalhosszúságú
oldalhosszúságú  tömegű téglalap alakú lemez függőlegesen elhelyezkedő
tömegű téglalap alakú lemez függőlegesen elhelyezkedő  oldala mentén levő tengely körül forog. A
oldala mentén levő tengely körül forog. A  időpontban szögsebessége
időpontban szögsebessége  . A lemez felületére a közegellenállás folytán erő hat, mely a mozgását akadályozza. Egy felületelemre ható erő arányos a felületelem sebességének négyzetével és a felületelem nagyságával, az arányossági tényező
. A lemez felületére a közegellenállás folytán erő hat, mely a mozgását akadályozza. Egy felületelemre ható erő arányos a felületelem sebességének négyzetével és a felületelem nagyságával, az arányossági tényező  .
.
- a) Mekkora a
 -ik időpillanatban a tengelytől
-ik időpillanatban a tengelytől  távolságban elhelyezkedő
távolságban elhelyezkedő 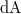 felületelemre ható, közegellenállásból származó erő?
felületelemre ható, közegellenállásból származó erő?
- b) Mekkora a lemezre ható nyomaték nagysága?
- c) Hogyan változik a lemez szöggyorsulása és szögsebessége az idő függvényében?
- d) Mekkora és hol van a támadáspontja az eredő közegellenállási erőnek?
- a) Mekkora a
- (3.2.13.) Egy homogén rúd tömege
 . Egyik végén átmenő vízszintes tengely körül elforoghat, a másik végén
. Egyik végén átmenő vízszintes tengely körül elforoghat, a másik végén  tömegű teher lóg. A rudat geometriai középpontjában ható
tömegű teher lóg. A rudat geometriai középpontjában ható 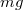 nagyságú vízszintes erővel húzzuk. Mekkora a rúd függőlegessel alkotott szöge egyensúly esetén?
nagyságú vízszintes erővel húzzuk. Mekkora a rúd függőlegessel alkotott szöge egyensúly esetén?
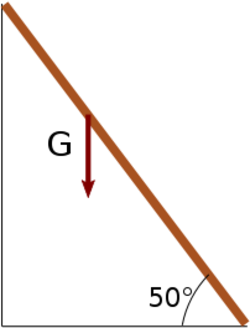
- (*3.2.14.) Egy
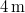 hosszú létrát függőleges falhoz támasztunk úgy, hogy a vízszintes talajjal
hosszú létrát függőleges falhoz támasztunk úgy, hogy a vízszintes talajjal 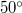 -os szöget zár be. A létra és a talaj közötti súrlódási együttható
-os szöget zár be. A létra és a talaj közötti súrlódási együttható 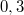 . A fal súrlódásmentes. Ha valaki a létrára mászik, milyen magasra jut, mielőtt a létra megcsúszik? (A létra tömegét hanyagoljuk el!)
. A fal súrlódásmentes. Ha valaki a létrára mászik, milyen magasra jut, mielőtt a létra megcsúszik? (A létra tömegét hanyagoljuk el!)
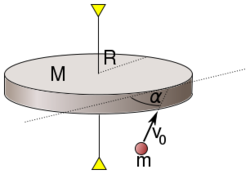
- Egy
 tömegű,
tömegű,  sugarú vízszintes korong a szimmetriatengelyén átmenő, függőleges tengely körül foroghat. A korong kezdetben áll. Egy
sugarú vízszintes korong a szimmetriatengelyén átmenő, függőleges tengely körül foroghat. A korong kezdetben áll. Egy  tömegű golyót lövünk a korongnak vízszintesen
tömegű golyót lövünk a korongnak vízszintesen 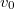 sebességgel úgy, hogy a sebességvektor a korong vízszintes érintőjével
sebességgel úgy, hogy a sebességvektor a korong vízszintes érintőjével  szöget zár be, ahogy az ábra is mutatja. A golyó és a korong tökéletesen rugalmatlanul ütközik, a golyó hozzátapad a koronghoz.
szöget zár be, ahogy az ábra is mutatja. A golyó és a korong tökéletesen rugalmatlanul ütközik, a golyó hozzátapad a koronghoz.
- a.) Mekkora lesz az ütközés után a korong szögsebessége?
- b.) Hányad része vész el a kezdeti mozgási energiának?
- c.) Legalább mekkora a golyó és korong közötti "ragasztó" erő?
- (3.2.15.) Közös tengely körül szabadon foroghat két tömör lendkerék, amelyek tömege
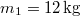 , és
, és 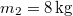 , átmérője
, átmérője 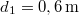 , és
, és 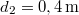 . A második
. A második 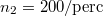 fordulatszámmal forog, az első áll. Mekkora közös fordulatszámmal haladnak, ha hirtelen egymással összekapcsoljuk őket?
fordulatszámmal forog, az első áll. Mekkora közös fordulatszámmal haladnak, ha hirtelen egymással összekapcsoljuk őket?
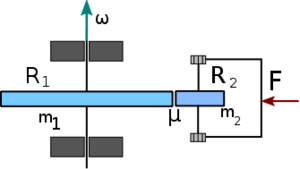
- (*3.2.16.) Egymással párhuzamosan elhelyezkedő tengely körül foroghat egy
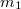 és egy
és egy 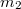 tömegű tárcsa, melyek sugarai rendre
tömegű tárcsa, melyek sugarai rendre  és
és  . Az
. Az  sugarú tárcsát
sugarú tárcsát 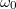 szögsebességgel megforgatjuk, majd az álló
szögsebességgel megforgatjuk, majd az álló  sugarú tárcsához nyomjuk
sugarú tárcsához nyomjuk  erővel. A tárcsák érintkező felületei között a súrlódási együttható
erővel. A tárcsák érintkező felületei között a súrlódási együttható  .
.
- a) Mennyi idő alatt érik el az együttforgás állapotát, és mekkora szögsebességgel forognak ekkor?
- b) Milyen értékűvé válik ez idő alatt a rendszer kinetikus energiája?
- c) Ellenőrizze az eredő impulzusmomentumot és annak változását. Mi okozza a változást?
- d) Milyen súrlódási tényező lenne energiatakarékosság szempontjából gazdaságos?
- (*3.2.17.) Az
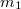 és
és 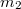 tömegű,
tömegű,  és
és  sugarú rögzített tengely körül forgó, homogén tömegeloszlású tárcsák elhanyagolható tömegű szíjjal kapcsolódnak egymáshoz. A hajtó tárcsára
sugarú rögzített tengely körül forgó, homogén tömegeloszlású tárcsák elhanyagolható tömegű szíjjal kapcsolódnak egymáshoz. A hajtó tárcsára 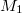 nagyságú forgatónyomaték hat, a másikat
nagyságú forgatónyomaték hat, a másikat 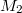 értékű nyomaték terheli. Feltételezzük, hogy a szíj a tárcsákon nem csúszik meg.
értékű nyomaték terheli. Feltételezzük, hogy a szíj a tárcsákon nem csúszik meg.
- a) Határozzuk meg mindkét tárcsa szöggyorsulását!
- b) Hogyan függ az
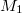 nyomatékot szolgáltató energiaforrás teljesítménye az időtől, ha a
nyomatékot szolgáltató energiaforrás teljesítménye az időtől, ha a  időpontban a tárcsák álltak?
időpontban a tárcsák álltak?
- c) Milyen teljesítménnyel végez munkát a terhelő szerkezet a
 -ik időpillanatban?
-ik időpillanatban?
- d) Mire fordítódik az
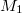 nyomatékot szolgáltató forrás energiájának és a terhelés által végzett munkának a különbsége?
nyomatékot szolgáltató forrás energiájának és a terhelés által végzett munkának a különbsége?
- Határozzuk meg egy
 tömegű,
tömegű,  oldalhosszúságú négyzet alakú homogén lemez tehetetlenségi nyomatékát a tömegközéppontján átmenő, rá merőleges tengelyre vonatkoztatva!
oldalhosszúságú négyzet alakú homogén lemez tehetetlenségi nyomatékát a tömegközéppontján átmenő, rá merőleges tengelyre vonatkoztatva!
![\[\beta=5\,\rm s^{-1}\]](/images/math/6/d/e/6de34b1a6a49a8494f2b9c6fc0db1369.png)
![\[\alpha=10\,\rm{rad}\]](/images/math/8/2/5/825c34cc3c15470b5c9142c00945b9c2.png)
![\[a=1\,\frac{\rm m}{\rm s^2}\]](/images/math/a/5/5/a550a7d7899a1174dfaebfa072c8a8b6.png)
![\[M=628\,\rm{Nm}\]](/images/math/9/e/b/9eb2134801f4c3896d8a6e575c5ff07a.png)
![\[F=157\,\rm{N}\]](/images/math/2/b/e/2bea2accd3bbd4d30e77898ae3b9d0f7.png)
![\[W_{F_s}=12377\,\rm J=1250\,\pi^2\,\rm J\]](/images/math/d/1/1/d118ed8c66e1bff8b7032653ff3e23a7.png)
![\[\theta=\frac75mR^2.\]](/images/math/9/b/f/9bfcef56b72d5fbd2e1ab88c826a893c.png)
![\[P(t)=\frac75mR^2\beta^2t.\]](/images/math/4/6/7/467595248901aee1cf9b42514dd518c2.png)
![\[\beta=\sqrt{\frac{P}{2\theta}} \frac1{\sqrt t}\]](/images/math/7/6/f/76f2b220a4740349f173edc2d51ce90e.png)
![\[T=2\pi\sqrt{\frac{7h}{12g}}\]](/images/math/7/b/8/7b81f643792cc1e9067aad908d91ec2b.png)
![\[T=2\pi\sqrt{\frac{3R}{2g}}\]](/images/math/4/e/a/4ea14b54cee73be1ca8f6026d8c03730.png)
![\[M=bk\omega^2(t)\frac{a^4}4\]](/images/math/f/d/b/fdb23ec6d17f009a90bfaac2ee8a40b1.png)
![\[\omega(t)=\frac{\omega_0}{1-\frac{a^4\omega_0bkt}{4\theta}}\]](/images/math/2/d/f/2df029841db4c1cdd4f719262e5a1b4f.png)
![\[F=bk\omega^2a^3/3\]](/images/math/a/9/7/a97afbfbe81ef8baabe4f30dfede92f8.png)
![\[R=\frac3 4 a\]](/images/math/a/5/d/a5d01429613568c067d14eade47f9336.png)
![\[\tan{\alpha}=\frac13\]](/images/math/6/f/4/6f474de104cff6e9567be50c186472d0.png)
![\[h=1,095\,\rm m\]](/images/math/5/a/a/5aabfcfdedb74b30d952796bac49d2d5.png)
![\[n=0,763\,\frac1{\rm s}\]](/images/math/f/7/0/f7087a1222f15d169b1560ce091293f6.png)
![\[t=\frac{\omega_0R_1m_1m_2}{2\mu F(m_1+m_2)}\]](/images/math/5/e/5/5e52cc73b7a567ae3d2db60e61a8e2c2.png)
![\[\omega_1=\omega_0\frac{m_1}{m_1+m_2}\]](/images/math/d/8/9/d89ba49c43c9b31f9d54831787a082f6.png)
![\[\omega_2=\omega_0\frac{R_1}{R_2}\frac{m_1}{m_1+m_2}\]](/images/math/8/d/0/8d052ce1a1f2d164ceccb740c9a1de9e.png)
![\[E=\frac14\omega_0R_1\frac{m_1}{m_1+m_2}(m_1R_1+m_2R_2)\]](/images/math/3/d/5/3d51e96c1f5a937b76de1be422c8da76.png)
![\[\Delta L=\frac12\frac{m_1m_2\omega_0(R_2R_1-R_1^2)}{m_1+m_2}\]](/images/math/f/c/3/fc3a5cfb7d2f78120e2e0a034d0ac156.png)
![\[\beta_1=\frac{M_1R_2^2-M_2R_1R_2}{\theta_2R_1^2+\theta_1R_1^2}\]](/images/math/d/d/3/dd39a46759aef91b219c6adeca59db19.png)
![\[\beta_2=\beta_1\frac{R_1}{R_2}\]](/images/math/c/c/1/cc160163c615604fe6077d54110040be.png)
![\[P_1=M_1\beta_1t\]](/images/math/6/7/2/672f3e300219d15381fb6ceac3b70771.png)
![\[P_2=M_2\beta_2t\]](/images/math/5/0/8/5085333ef0b408f5dd6109ddb9f084b9.png)
![\[\Theta = \frac{1}{6} m L^2\]](/images/math/3/2/5/325dc90414683c3eec6ec353c048c9c0.png)