Elektrosztatika példák - Határfelületen kialakult töltéssűrűség
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Csorean (vitalap | szerkesztései) 2021. március 22., 14:26-kor történt szerkesztése után volt.
Feladat
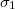 és
és 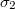 vezetőképességű anyagok érintkező felületén normális irányú áramsűrűség folyik át. Határozzuk meg a felületi töltéssűrűséget!
vezetőképességű anyagok érintkező felületén normális irányú áramsűrűség folyik át. Határozzuk meg a felületi töltéssűrűséget!
Megoldás
Írjuk fel a kontinuitási egyenletet a közeghatárra:
![\[j_1\cdot A = j_2\cdot A \rightarrow j_1 = j_2 = j\]](/images/math/a/0/c/a0c26414fdcfc87dc9688cfc6849b5e9.png)
Tehát az áramsűrűség megegyezik mindkét közegben. Ha felírjuk a differenciális Ohm-törvényt mindkét közegben:
![\[j =\sigma_1\cdot E_1 \]](/images/math/d/7/b/d7b38b85552942e392fb0a619f243549.png)
![\[j =\sigma_2\cdot E_2 \]](/images/math/5/1/0/5105b6f33996b6023356f67499d4645f.png)
Amiből
![\[E_2 = \frac{\sigma_1}{\sigma_2}\cdot E_1\]](/images/math/8/0/0/8008fd89e38cc83cf792d7ccfa0a3526.png)
A határfelületen felhalmozódott felületi töltéssűrűséget úgy kaphatjuk meg, ha felveszünk egy téglatest alakú zárt felületet, melynek két oldala párhuzamos a határfelülettel, továbbá a közeghatár  területű részét magába zárja. Erre felírjuk a Gauss-tételt:
területű részét magába zárja. Erre felírjuk a Gauss-tételt:
![\[E_2 A-E_1 A = \frac{Q}{\epsilon_0} = \frac{\omega}{\epsilon_0}\cdot A \]](/images/math/8/a/b/8ab48565dff1a8f9ddb693de065d9c52.png)
Ebből a felületen felhalmozódott töltéssűrűség:
![\[\omega = \epsilon_0 j \cdot\left(\frac{1}{\sigma_2}-\frac{1}{\sigma_1}\right)\]](/images/math/7/9/0/790bd5db1a88763155f85fdfda7944b4.png)