„Elektrosztatika példák - Áramvonalak törési törvénye” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Elektrosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
(→Megoldás) |
||
| 12. sor: | 12. sor: | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| − | Legyen $\alpha_1$ és $\alpha_2$ az áramvonalaknak a | + | Legyen $\alpha_1$ és $\alpha_2$ az áramvonalaknak a közeghatár normálisával bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó. |
$$\vec{j_1}\cdot\vec{A} =\vec{j_2}\cdot\vec{A} \rightarrow j_1\cos\left(\alpha_1\right) = j_2\cos\left(\alpha_2\right) $$ | $$\vec{j_1}\cdot\vec{A} =\vec{j_2}\cdot\vec{A} \rightarrow j_1\cos\left(\alpha_1\right) = j_2\cos\left(\alpha_2\right) $$ | ||
| − | Az örvénymentességből pedig következik, hogy az elektromos tér | + | Az örvénymentességből pedig következik, hogy az elektromos tér felülettel párhuzamos komponense folytonosan megy át: |
$$E_{1t} = E_{2t} $$ | $$E_{1t} = E_{2t} $$ | ||
| − | + | Ezen összefüggésbe behelyettesítve a differenciális Ohm-törvényt: | |
$$\frac{j_1 \sin\left(\alpha_1\right)}{\sigma_1} = \frac{j_2 \sin\left(\alpha_2\right)}{\sigma_2}$$ | $$\frac{j_1 \sin\left(\alpha_1\right)}{\sigma_1} = \frac{j_2 \sin\left(\alpha_2\right)}{\sigma_2}$$ | ||
| − | A | + | A határfelületre merőleges és párhuzamos áramsűrűség-komponensekre felírt egyenletek hányadosát véve megkapjuk a törési törvényt: |
$$\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)$$ | $$\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. szeptember 14., 21:17-kori változata
Feladat
- Határozzuk meg az áramvonalak törési törvényét a
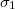és 
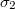vezetőképességű közegek határán.
Megoldás
Legyen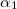 
és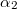 
az áramvonalaknak a közeghatár normálisával bezárt szöge a két közegben. A kontinuitási törvény értelmében az áramvonalak határfelületre merőleges komponense állandó.
![\[\vec{j_1}\cdot\vec{A} =\vec{j_2}\cdot\vec{A} \rightarrow j_1\cos\left(\alpha_1\right) = j_2\cos\left(\alpha_2\right) \]](/images/math/8/2/7/827afd735af94c884dc0fc233fb2b9ca.png)
Az örvénymentességből pedig következik, hogy az elektromos tér felülettel párhuzamos komponense folytonosan megy át:
![\[E_{1t} = E_{2t} \]](/images/math/d/5/9/d59760c33230de53eb5d60da46323704.png)
Ezen összefüggésbe behelyettesítve a differenciális Ohm-törvényt:
![\[\frac{j_1 \sin\left(\alpha_1\right)}{\sigma_1} = \frac{j_2 \sin\left(\alpha_2\right)}{\sigma_2}\]](/images/math/0/2/9/029ee907ef9cee8ec9ebb36074712905.png)
A határfelületre merőleges és párhuzamos áramsűrűség-komponensekre felírt egyenletek hányadosát véve megkapjuk a törési törvényt:
![\[\sigma_1\cdot\cot\left(\alpha_1\right) = \sigma_2\cdot\cot\left(\alpha_2\right)\]](/images/math/a/9/b/a9b91a5d5a4e80746e75088230a80969.png)
