„Elektrosztatika példák - Vezető anyaggal töltött kondenzátor ellenállása” változatai közötti eltérés
(→Megoldás) |
(→Megoldás) |
||
| 15. sor: | 15. sor: | ||
$$E\cdot 4 \pi r^2 = \frac{Q}{\epsilon_0}$$ | $$E\cdot 4 \pi r^2 = \frac{Q}{\epsilon_0}$$ | ||
$$E = \frac{Q}{4\pi r^2 \epsilon_0}$$ | $$E = \frac{Q}{4\pi r^2 \epsilon_0}$$ | ||
| − | + | amiből a gömbök közötti potenciálkülönbség: | |
$$U = \int_a ^b \vec{E}\cdot\vec{dr} = \frac{Q}{4\pi\epsilon_0}\cdot\left(\frac{1}{a}-\frac{1}{b}\right)$$ | $$U = \int_a ^b \vec{E}\cdot\vec{dr} = \frac{Q}{4\pi\epsilon_0}\cdot\left(\frac{1}{a}-\frac{1}{b}\right)$$ | ||
A differenciális Ohm-törvény alapján a gömbben folyó áramsűrűség nagysága: | A differenciális Ohm-törvény alapján a gömbben folyó áramsűrűség nagysága: | ||
$$j = \sigma\cdot E$$ | $$j = \sigma\cdot E$$ | ||
$$j = \frac{\sigma Q}{4 \pi r^2 \epsilon_0}$$ | $$j = \frac{\sigma Q}{4 \pi r^2 \epsilon_0}$$ | ||
| − | + | amely áramsűrűséget az $r$ sugarú gömbfelületen integrálva megkapjuk a gömbhéjak között folyó áramot: | |
$$I = \iint \vec{j}\cdot\vec{dA} = \frac{\sigma Q}{\epsilon_0}$$ | $$I = \iint \vec{j}\cdot\vec{dA} = \frac{\sigma Q}{\epsilon_0}$$ | ||
Ebből az Ohm-törvény alapján a gömb ellenállása: | Ebből az Ohm-törvény alapján a gömb ellenállása: | ||
A lap 2013. szeptember 27., 15:08-kori változata
Feladat
- Számítsuk ki az
a)
és 
sugarú gömblemezekből álló 
, 
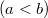vezetőképességű közeggel kitöltött gömbkondenzátor; ill.
b) az
élhosszúságú, és sugarú, henger alakú lemezekből álló, vezetőképességű közeggel kitöltött hengerkondenzátor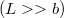 
ellenállását!
Megoldás
a, A Gauss-tétel stacionárius áramok esetén is igaz. Azt feltételezzük, hogy a külső és belső gömbhéjakon töltések halmozódnak fel, amelyek létrehozzák a potenciálkülönbséget. A Gauss tétel egy 
sugarú koncentrikus gömbre:
![\[E\cdot 4 \pi r^2 = \frac{Q}{\epsilon_0}\]](/images/math/e/e/c/eec550b215ecc9c025f2fbdda5fe7044.png)
![\[E = \frac{Q}{4\pi r^2 \epsilon_0}\]](/images/math/7/7/4/774228dcf9268347a02d13746b336a50.png)
amiből a gömbök közötti potenciálkülönbség:
![\[U = \int_a ^b \vec{E}\cdot\vec{dr} = \frac{Q}{4\pi\epsilon_0}\cdot\left(\frac{1}{a}-\frac{1}{b}\right)\]](/images/math/2/c/3/2c303d40a7606031daeeea2752aa8653.png)
A differenciális Ohm-törvény alapján a gömbben folyó áramsűrűség nagysága:
![\[j = \sigma\cdot E\]](/images/math/8/6/b/86bbd6765bce799aa90ef27931689d6f.png)
![\[j = \frac{\sigma Q}{4 \pi r^2 \epsilon_0}\]](/images/math/0/c/6/0c6214a2b9472ddb54a0b7abddbc2b92.png)
amely áramsűrűséget az sugarú gömbfelületen integrálva megkapjuk a gömbhéjak között folyó áramot:
![\[I = \iint \vec{j}\cdot\vec{dA} = \frac{\sigma Q}{\epsilon_0}\]](/images/math/5/4/1/541fff2f50a1117429074589b9ba6e18.png)
Ebből az Ohm-törvény alapján a gömb ellenállása:
![\[R = \frac{U}{I} = \frac{1}{4 \pi\sigma}\cdot\frac{b-a}{ab}\]](/images/math/8/4/e/84e92eab27c675b0f15ff3e48ae19305.png)
b, A Gauss-tétel stacionárius áramok esetén is igaz. Azt feltételezzük, hogy a külső és belső hengerfelületeken töltések halmozódnak fel, amelyek létrehozzák a potenciálkülönbséget. A Gauss-tétel egy sugarú koncentrikus hengerre:
![\[E\cdot 2 \pi r L = \frac{Q}{\epsilon_0}\]](/images/math/b/3/b/b3b7f1acbe2ca5272eef8031a136800b.png)
![\[E = \frac{Q}{4\pi r L \epsilon_0}\]](/images/math/0/1/c/01c1f0300f3d2b18bef40272629e0e30.png)
Amiből a hengerek közötti potenciálkülönbség:
![\[U = \int_a ^b \vec{E}\cdot\vec{dr} = \frac{Q}{2\pi\epsilon_0 L}\cdot\ln\left(\frac{b}{a}\right)\]](/images/math/f/8/a/f8a9196d3ea05e05eaf7aff67fb2fd29.png)
A differenciális Ohm-törvény alapján a hengerben folyó áramsűrűség:
![\[\vec{j} = \sigma\cdot\vec{E}\]](/images/math/0/0/e/00ebb810bd08d4ee3f75e9afb38ce9a0.png)
![\[\vec{j} = \frac{\sigma Q}{2 \pi r L \epsilon_0}\]](/images/math/c/c/9/cc9288e825706f7e309e16d0a62eebad.png)
Amely áramsűrűséget az sugarú hengerfelületen integrálva megkapjuk a hengerek között folyó áramot:
Ebből az Ohm-törvény alapján a henger ellenállása:
![\[R = \frac{U}{I} = \frac{\ln\left(\frac{b}{a}\right)}{2 \pi L\sigma}\]](/images/math/2/c/0/2c03bec5c484c7acbeff168450f84864.png)
