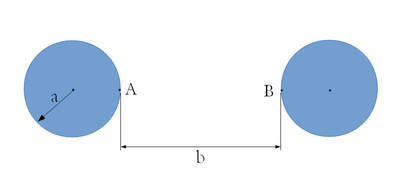
Elektrosztatika példák - Két azonos sugarú fémgömbből álló rendszer kapacitása
Feladat
- Mekkora két azonos ,
sugarú fémgömbből álló rendszer kapacitása, ha gömbök felületének egymáshoz legközelebbi pontjai 
távolságra helyezkednek el? (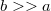
)
Megoldás
Legyen 
töltése az egyik, 
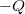töltése a másik fémgömbnek.
Gauss tétel segítségével könnyen meghatározhatjuk a töltésű gömb által keltett teret az 
távolság függvényében:
![\[E_{(r)}=\dfrac{Q}{4\pi \varepsilon_0}\dfrac{1}{r^2}\]](/images/math/c/4/2/c425a5ac87e20defd544eff4d5293063.png)
A töltéssel bíró gömb által keltett tér hatására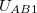 
potenciálkülönbség jön létre az ábrán látható A és B pontok között. Mivel a gömbfelületek külön-külön ekvipotenciális felületek, emiatt a két gömbfelületnek bármely két pontja között azonos a feszültség. Az 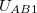meghatározható, ha a gömb elektromos terét integráljuk 
és 
pontok között:
![\[U_{AB1}=-\int_{A}^{B}E_{(r)}dr=-\int_{a}^{b+a}E_{(r)}dr=-\dfrac{Q}{4\pi \varepsilon_0} \int_{a}^{b+a} \dfrac{1}{r^2} dr=\dfrac{Q}{4\pi \varepsilon_0} \left( \dfrac{1}{a}-\dfrac{1}{b+a} \right)\]](/images/math/4/b/d/4bd882d1a173cf2ab7be348a79768901.png)
A két gömbből álló rendszer tükörszimmetriájából következik, hogy a másik, 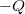töltésű gömb által az és pontok között létrehozott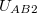 
potenciálkülönbség megegyezik az első gömb által keltett 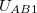potenciálkülönbséggel. (
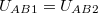) Tekintve, hogy a potenciáltér lineáris, a két gömbfelület között mért potenciálkülönbség az egyes gömbök által keltett potenciálkülönbségek összege:
![\[U_{AB}=U_{AB1}+U_{AB2}=2U_{AB1}=\dfrac{Q}{2\pi \varepsilon_0} \left( \dfrac{1}{a}-\dfrac{1}{b+a} \right)\]](/images/math/b/4/b/b4b2e311fc778044a032931d40f9b75f.png)
A rendszer kapacitása:
![\[C=\dfrac{Q}{U_{AB}}=\dfrac{2\pi \varepsilon_0}{\left( \dfrac{1}{a}-\dfrac{1}{b+a} \right)}\]](/images/math/b/c/1/bc1bcd75daaed0ced276f18a67cae66c.png)
