Mechanika - Lépcsős csiga
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
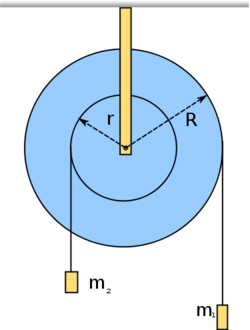
Feladat
- (*3.3.8.) Az ábrán feltüntetett
 tehetetlenségi nyomatékú lépcsős csiga két kötelére
tehetetlenségi nyomatékú lépcsős csiga két kötelére 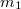 és
és 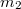 tömegű súlyokat függesztünk. Határozzuk meg a csiga szöggyorsulását, és a kötélágakban ébredő erőket!
tömegű súlyokat függesztünk. Határozzuk meg a csiga szöggyorsulását, és a kötélágakban ébredő erőket!
Megoldás
A mozgásegyenletek:![\[m_1a_1=m_1g-K_1\]](/images/math/5/2/9/52950dab6f7ac98bc9efdd8ae8014efe.png)
![\[m_2a_2=m_2g-K_2\]](/images/math/6/0/d/60d2d441a25e00875fefd86ce663bf4d.png)
![\[K_1R-K_2r=\theta\beta,\]](/images/math/5/3/7/5377d5fa5cd7477e83069c5f0a2cd8d1.png)
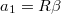 és
és 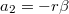 . Áttérve a szöggyorsulásra és a kötélerőket kiejtve kapjuk
. Áttérve a szöggyorsulásra és a kötélerőket kiejtve kapjuk ![\[\beta=\frac{m_1gR-m_2gr}{m_1R^2+m_2r^2+\theta},\]](/images/math/0/1/5/015c575e4d0c93e7adb6c6f44ea3c309.png)
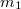 és
és 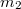 tömeget nulla hosszúságú kötéllel rögzítettnek képzeljük a tárcsán, ugyanis
tömeget nulla hosszúságú kötéllel rögzítettnek képzeljük a tárcsán, ugyanis  nevezőjében épp az így képzett test tehetetlenségi nyomatéka látható, a számlálóban pedig a két súlyerő nyomatéka a megfelelő szöghelyzetben!
nevezőjében épp az így képzett test tehetetlenségi nyomatéka látható, a számlálóban pedig a két súlyerő nyomatéka a megfelelő szöghelyzetben!