„Mechanika - Lelógatott korong” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
(→Megoldás) |
||
| 12. sor: | 12. sor: | ||
#: b) Mekkora a korong $\omega$ szögsebessége és középpontjának $v$ sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról $l$ hosszúságú fonaldarab csavarodott le? ÁBRA</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\beta=\frac{2g}{3R}$$ $$K=\frac{mg}3$$ $$\omega=\sqrt{\frac{4gl}{3R^2}}$$ $$v=\sqrt{\frac43 gl}$$}}</wlatex></includeonly><noinclude> | #: b) Mekkora a korong $\omega$ szögsebessége és középpontjának $v$ sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról $l$ hosszúságú fonaldarab csavarodott le? ÁBRA</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\beta=\frac{2g}{3R}$$ $$K=\frac{mg}3$$ $$\omega=\sqrt{\frac{4gl}{3R^2}}$$ $$v=\sqrt{\frac43 gl}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A mozgásegyenletek $$ma=mg-K$$ illetve $$\theta_{\rm{TKP}}\beta=KR,$$ ahol $mg$ a korong középpontjában támadó lefelé irányuló nehézségi erő, és $K$ a kerületén támadó, fölfelé irányuló kötélerő, $\theta_{\rm{TKP}}=\frac12mR^2$ pedig a tömegközéppontra vonatkozó tehetetlenségi nyomaték. Az lecsavarodó fonálból adódik, hogy $a=R\beta$. Az egyenleteket $\beta$-ra és $K$-ra megoldva kapjuk $$\beta=\frac{2g}{3R}$$ és $$K=\frac{mg}3$$ megoldásokat. Ha a fonál $l$ hosszon csavarodott le, a tömegközéppont is ennyivel került lejjebb. A gyorsulások viszonya miatt $v=\omega R$, és az energiamegmaradás $$mgl=\frac12 \theta \omega^2$$ ahol $\theta=\frac32 mR^2$ a pillanatnyi forgáspontra nézve. A jobb oldalon álló forgási energia megegyezik a tömegközéppont mozgási, és az akörüli forgási energiával, ahol azonban a tömegközépponti tehetetlenségi nyomatékot kell használni! Végül $$\omega=\sqrt{\frac{4gl}{3R^2}}$$ $$v=\sqrt{\frac43 gl}$$</wlatex> | + | <wlatex>A mozgásegyenletek $$ma=mg-K$$ illetve $$\theta_{\rm{TKP}}\beta=KR,$$ ahol $mg$ a korong középpontjában támadó lefelé irányuló nehézségi erő, és $K$ a kerületén támadó, fölfelé irányuló kötélerő, $\theta_{\rm{TKP}}=\frac12mR^2$ pedig a tömegközéppontra vonatkozó tehetetlenségi nyomaték. Az lecsavarodó fonálból adódik, hogy $a=R\beta$. Az egyenleteket $\beta$-ra és $K$-ra megoldva kapjuk $$\beta=\frac{2g}{3R}$$ és $$K=\frac{mg}3$$ megoldásokat. Ha a fonál $l$ hosszon csavarodott le, a tömegközéppont is ennyivel került lejjebb. A gyorsulások viszonya miatt $v=\omega R$, és az energiamegmaradás $$mgl=\frac12 \theta \omega^2$$ ahol $\theta=\frac32 mR^2$ a pillanatnyi forgáspontra nézve. A jobb oldalon álló forgási energia megegyezik a tömegközéppont mozgási, és az akörüli forgási energiával, ahol azonban a tömegközépponti tehetetlenségi nyomatékot kell használni! Végül $$\omega=\sqrt{\frac{4gl}{3R^2}}$$ $$v=\sqrt{\frac43 gl}$$ |
| + | [[Kép:3.3.6.svg|none|250px]]</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. június 20., 12:58-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (3.3.6.)
 sugarú
sugarú  tömegű korong kerületére csavart fonál végét rögzítjük, és a korongot elengedjük.
tömegű korong kerületére csavart fonál végét rögzítjük, és a korongot elengedjük.
- a) Írjuk le a korong mozgását!
- b) Mekkora a korong
 szögsebessége és középpontjának
szögsebessége és középpontjának  sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról
sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról  hosszúságú fonaldarab csavarodott le? ÁBRA
hosszúságú fonaldarab csavarodott le? ÁBRA
Megoldás
A mozgásegyenletek![\[ma=mg-K\]](/images/math/e/2/2/e22302ddebe0869cc2c18e478e070415.png)
![\[\theta_{\rm{TKP}}\beta=KR,\]](/images/math/3/f/1/3f193bdce74088c14c795bf11a902979.png)
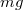 a korong középpontjában támadó lefelé irányuló nehézségi erő, és
a korong középpontjában támadó lefelé irányuló nehézségi erő, és  a kerületén támadó, fölfelé irányuló kötélerő,
a kerületén támadó, fölfelé irányuló kötélerő, 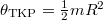 pedig a tömegközéppontra vonatkozó tehetetlenségi nyomaték. Az lecsavarodó fonálból adódik, hogy
pedig a tömegközéppontra vonatkozó tehetetlenségi nyomaték. Az lecsavarodó fonálból adódik, hogy 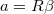 . Az egyenleteket
. Az egyenleteket  -ra és
-ra és  -ra megoldva kapjuk
-ra megoldva kapjuk ![\[\beta=\frac{2g}{3R}\]](/images/math/c/6/a/c6af796891b7a163698d29903524966c.png)
![\[K=\frac{mg}3\]](/images/math/5/2/7/52725fae775e2fae11b0ff221c1c53ea.png)
 hosszon csavarodott le, a tömegközéppont is ennyivel került lejjebb. A gyorsulások viszonya miatt
hosszon csavarodott le, a tömegközéppont is ennyivel került lejjebb. A gyorsulások viszonya miatt 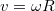 , és az energiamegmaradás
, és az energiamegmaradás ![\[mgl=\frac12 \theta \omega^2\]](/images/math/0/a/c/0ac4e93f5b9010e74bbdcbf2d1a22990.png)
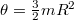 a pillanatnyi forgáspontra nézve. A jobb oldalon álló forgási energia megegyezik a tömegközéppont mozgási, és az akörüli forgási energiával, ahol azonban a tömegközépponti tehetetlenségi nyomatékot kell használni! Végül
a pillanatnyi forgáspontra nézve. A jobb oldalon álló forgási energia megegyezik a tömegközéppont mozgási, és az akörüli forgási energiával, ahol azonban a tömegközépponti tehetetlenségi nyomatékot kell használni! Végül ![\[\omega=\sqrt{\frac{4gl}{3R^2}}\]](/images/math/5/9/d/59d2cc5504905104ac1e8e187ab1e258.png)
![\[v=\sqrt{\frac43 gl}\]](/images/math/5/7/a/57a92411e8d0a4b01ec5b3e9920a3958.png)
