„Elektrosztatika példák - Dielektriumba helyezett fémgömb potenciáltere” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 2. Kategória:Szerkesztő:Beleznai Kategória:Elektrosztatika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 9. sor: | 9. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Egy $R_1$ sugarú, egyenletesen töltött. fémgömböt, egy $d$ vastag $\epsilon_r$ permittivitásű szigetelővel veszünk körbe. Hogyan függ a potenciál a centrumtól mért távolságtól? | </noinclude><wlatex># Egy $R_1$ sugarú, egyenletesen töltött. fémgömböt, egy $d$ vastag $\epsilon_r$ permittivitásű szigetelővel veszünk körbe. Hogyan függ a potenciál a centrumtól mért távolságtól? | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content= | + | </wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk a Gauss tételt a különböző tartományokra!}}{{Végeredmény|content=Vagyis ha $R_2<r$ akkor $$U = \frac{Q}{4\cdot\pi\cdot r\cdot\epsilon_0\cdot}$$ Ha $R_1<r<R_2$ akkor $$U = \frac{Q}{4\cdot\pi\cdot R_2\cdot\epsilon_0\cdot}+\frac{Q}{4\cdot\pi\cdot\epsilon_0\cdot\epsilon_r}\cdot\left(\frac{1}{r}-\frac{1}{R_2}\right)$$ A gömb belsejében pedig konstans ptenciál van, amelynek értéke: $$U = \frac{Q}{4\cdot\pi\cdot R_2\cdot\epsilon_0\cdot}+\frac{Q}{4\cdot\pi\cdot\epsilon_0\cdot\epsilon_r}\cdot\left(\frac{1}{R_1}-\frac{1}{R_2}\right) $$}} |
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
A lap 2013. június 26., 16:57-kori változata
Feladat
- Egy
sugarú, egyenletesen töltött. fémgömböt, egy 
vastag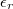 
permittivitásű szigetelővel veszünk körbe. Hogyan függ a potenciál a centrumtól mért távolságtól?
Megoldás
Legyen a külső gömb sugara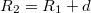 
, töltése pedig 
. Írjuk fel a Gauss-tételt, egy 
sugarú gömbre, amely koncentrikus -el és 
-vel.
![\[\iint\vec{D}\cdot{dA} = Q\]](/images/math/8/4/c/84c56138ae360f67febc7bb6936d1848.png)
Ha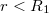 
akkor 
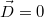és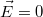 
hiszen az integrálási tartományon belül nem található töltés.
Ha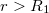 
, akkor
![\[D\cdot 4\cdot\pi\cdot r = Q \Rightarrow D = \frac{Q}{4\cdot\pi\cdot r^2}\]](/images/math/d/0/3/d03aba85906f9e85076002f51f545dc3.png)
Az elektromos tér pedig, mivel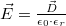 
ezért
ha
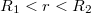akkor
![\[E = \frac{Q}{4\cdot\pi\cdot r^2\cdot\epsilon_0\cdot\epsilon_r}\]](/images/math/3/1/9/319b7dca9fe4391208a51aefc800d65a.png)
ha pedig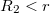 
akkor
![\[E = \frac{Q}{4\cdot\pi\cdot r^2\cdot\epsilon_0}\]](/images/math/c/b/2/cb22650fa44a9c28ccb7f4eddc0e26c0.png)
A potenciál az függvényében pedig:
![\[U\left(r\right) = -\int_\infty^r E\left(\tilde{r}\right)\cdot d\tilde{r}\]](/images/math/b/6/6/b661043d7f9bef946c0d299f00c3f46e.png)
Vagyis ha 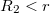akkor
![\[U = \frac{Q}{4\cdot\pi\cdot r\cdot\epsilon_0\cdot}\]](/images/math/a/f/0/af0807207b916b59efa499876d00de24.png)
Ha 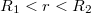akkor
![\[U = \frac{Q}{4\cdot\pi\cdot R_2\cdot\epsilon_0\cdot}+\frac{Q}{4\cdot\pi\cdot\epsilon_0\cdot\epsilon_r}\cdot\left(\frac{1}{r}-\frac{1}{R_2}\right)\]](/images/math/4/2/f/42fea07df3ecaebb14ec25042ea7bf1d.png)
A gömb belsejében pedig konstans ptenciál van, amelynek értéke:
![\[U = \frac{Q}{4\cdot\pi\cdot R_2\cdot\epsilon_0\cdot}+\frac{Q}{4\cdot\pi\cdot\epsilon_0\cdot\epsilon_r}\cdot\left(\frac{1}{R_1}-\frac{1}{R_2}\right) \]](/images/math/c/3/a/c3a22f84c1c1c89b99eaa62167b22f14.png)
A potenciált ábrázolva, egy folytonos görbét kapunk: 1.ábra
