„Mechanika - Korong vízszintes talajon húzva” változatai közötti eltérés

A lap 2013. július 1., 10:32-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) ← Régebbi szerkesztés		A lap 2013. augusztus 26., 13:19-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) a (→‎Megoldás) Újabb szerkesztés →
15. sor:		15. sor:
	== Megoldás ==		== Megoldás ==
−	<wlatex>A mozgásegyenletek $$ma=F-F_s$$ és $$\theta\beta=\frac12mR^2\cdot\frac aR=Fr+F_sR$$ feltéve, hogy az ismeretlen nagyságú tapadási súrlódási erő, amely a gördülést biztosítja, ellentétes irányú $F$ húzóerővel. A másik ismeretlenre, a gyorulásra, a gördülés miatt felírható, hogy $a=\beta R$, a tapadási súrlódási erőre pedig a $|F_s|\leq\mu mg$ reláció kell teljesüljön. A mozgásegyenletekből a súrlódási erőt kiejtve kapjuk $$a=\frac{2F(R+r)}{3mR}$$ kifejezést, amely pozitív, tehát a korong a rajzon jobbra gördül. A súrlódási erő kifejezése $$F_s=F\left(1-\frac{2(R+r)}{3R} \right )$$ Ha a zárójeles kifejezés pozitív, azaz $$1>\frac{2(R+r)}{3R},$$ akkor a súrlódási erő pozitív, azaz valóban a feltételezett irányú, és a tömegközéppont mozgásegyenletét tekintve fékező jellegű, emiatt $a<\frac Fm$. A fenti reláció akkor teljesül, ha $R>2r$.	+	<wlatex>A mozgásegyenletek $$ma=F-F_s$$ és $$\theta\beta=\frac12mR^2\cdot\frac aR=Fr+F_sR$$ feltéve, hogy az ismeretlen nagyságú tapadási súrlódási erő, amely a gördülést biztosítja, ellentétes irányú $F$ húzóerővel. A másik ismeretlenre, a gyorsulásra, a gördülés miatt felírható, hogy $a=\beta R$, a tapadási súrlódási erőre pedig a $|F_s|\leq\mu mg$ reláció kell teljesüljön. A mozgásegyenletekből a súrlódási erőt kiejtve kapjuk $$a=\frac{2F(R+r)}{3mR}$$ kifejezést, amely pozitív, tehát a korong a rajzon jobbra gördül. A súrlódási erő kifejezése $$F_s=F\left(1-\frac{2(R+r)}{3R} \right )$$ Ha a zárójeles kifejezés pozitív, azaz $$1>\frac{2(R+r)}{3R},$$ akkor a súrlódási erő pozitív, azaz valóban a feltételezett irányú, és a tömegközéppont mozgásegyenletét tekintve fékező jellegű, emiatt $a<\frac Fm$. A fenti reláció akkor teljesül, ha $R>2r$.
	$R<2r$ esetén a két erő azonos irányú, és $a>\frac Fm$ (!), tehát a súrlódási erő segíti a korong gyorsítását. Speciális esetben, ha $R=2r$, $F_s=0$ adódik, tehát súrlódás nélkül is lehet gördülés tetszőleges húzóerő mellett. Egyéb esetekben a húzóerő és a tapadási súrlódási együttható között fenn kell álljon egy reláció. A súrlódási erő kifejezését továbírva $$F_s=F\frac{R-2r}{3R},$$ így $$F\frac{|R-2r|}{3R}\leq\mu mg,$$ amely adott $\mu$-re az erőt maximálja, adott erő mellett pedig minimumot ad rá nézve.		$R<2r$ esetén a két erő azonos irányú, és $a>\frac Fm$ (!), tehát a súrlódási erő segíti a korong gyorsítását. Speciális esetben, ha $R=2r$, $F_s=0$ adódik, tehát súrlódás nélkül is lehet gördülés tetszőleges húzóerő mellett. Egyéb esetekben a húzóerő és a tapadási súrlódási együttható között fenn kell álljon egy reláció. A súrlódási erő kifejezését továbírva $$F_s=F\frac{R-2r}{3R},$$ így $$F\frac{|R-2r|}{3R}\leq\mu mg,$$ amely adott $\mu$-re az erőt maximálja, adott erő mellett pedig minimumot ad rá nézve.
	Ha a korong közepe alatt húzzuk a kötelet, a nyomatéki egyenletben az $Fr$ tag előjelet vált, ezért a gyorsulás kifejezése most $$a=\frac{2F(R-r)}{3mR},$$ ami továbbra is pozitív, viszont $$F_s=F\frac{R+2r}{3R}$$ mindig pozitív, azaz $a<\frac Fm$, a súrlódás mindig fékező hatású lesz. $$F\frac{R+2r}{3R}\leq\mu mg$$</wlatex>		Ha a korong közepe alatt húzzuk a kötelet, a nyomatéki egyenletben az $Fr$ tag előjelet vált, ezért a gyorsulás kifejezése most $$a=\frac{2F(R-r)}{3mR},$$ ami továbbra is pozitív, viszont $$F_s=F\frac{R+2r}{3R}$$ mindig pozitív, azaz $a<\frac Fm$, a súrlódás mindig fékező hatású lesz. $$F\frac{R+2r}{3R}\leq\mu mg$$</wlatex>
	</noinclude>		</noinclude>

---

A lap 2013. augusztus 26., 13:19-kori változata

[rejt] Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Merev testek II.
Feladatok listája: Korongon mozgatott tömegpont Lelógatott korong Lelógatott korong tárcsával és tömeggel Lépcsős csiga Tömeg rugón súlyos csigával Korong vízszintes talajon húzva Henger lejtőn Három test lejtőn Forgó henger lejtőn húzva Hokikorong és rúd ütközése Hokikorong és rúd ütközése II Felbillenés lejtőn
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

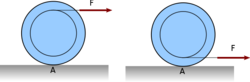
1. (*3.3.13.) Vízszintes lapon álló tömegű koronghoz erősített elhanyagolható tömegű tárcsa kerületére csavart fonalat vízszintes irányban állandó erővel húzunk. A korong sugara , a tárcsa sugara .(A fonalat a korong középpontja fölött húzzuk.)
   

   a) Mekkora gyorsulással mozog a korong középpontja?

   b) Mi a talaj és a korong között fellépő súrlódási erő szerepe a korong középpontjának gyorsításánál?

   c) Mekkora 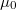súrlódási együttható szükséges ahhoz, hogy a korong a talajon csúszás nélkül gördülhessen?

   d) Oldjuk meg a feladatot arra az esetre is, ha a fonalat a korong középpontja alatt húzzuk a talaj síkjával párhuzamosan!

Megoldás

A mozgásegyenletek és feltéve, hogy az ismeretlen nagyságú tapadási súrlódási erő, amely a gördülést biztosítja, ellentétes irányú húzóerővel. A másik ismeretlenre, a gyorsulásra, a gördülés miatt felírható, hogy 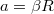, a tapadási súrlódási erőre pedig a 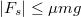reláció kell teljesüljön. A mozgásegyenletekből a súrlódási erőt kiejtve kapjuk kifejezést, amely pozitív, tehát a korong a rajzon jobbra gördül. A súrlódási erő kifejezése Ha a zárójeles kifejezés pozitív, azaz akkor a súrlódási erő pozitív, azaz valóban a feltételezett irányú, és a tömegközéppont mozgásegyenletét tekintve fékező jellegű, emiatt . A fenti reláció akkor teljesül, ha 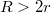. 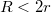esetén a két erő azonos irányú, és 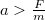(!), tehát a súrlódási erő segíti a korong gyorsítását. Speciális esetben, ha 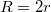, 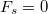adódik, tehát súrlódás nélkül is lehet gördülés tetszőleges húzóerő mellett. Egyéb esetekben a húzóerő és a tapadási súrlódási együttható között fenn kell álljon egy reláció. A súrlódási erő kifejezését továbírva így amely adott -re az erőt maximálja, adott erő mellett pedig minimumot ad rá nézve. Ha a korong közepe alatt húzzuk a kötelet, a nyomatéki egyenletben az 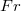tag előjelet vált, ezért a gyorsulás kifejezése most ami továbbra is pozitív, viszont mindig pozitív, azaz , a súrlódás mindig fékező hatású lesz.