„Mechanika - Három test lejtőn” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
a (→Megoldás) |
||
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (3.3.17.) A vízszintessel $30^{\circ}$-os szöget képező $5\,\rm m$ magasságú lejtőn egyidejűleg kezdősebesség nélkül elindítunk egy hasábot, egy hengert és egy golyót. A hasáb súrlódásmentesen csúszik, a henger és a golyó csúszásmentesen gördül. A testek különböző időtartamok alatt érnek a lejtő aljára, ahol lécbe ütköznek. Mekkora időközök telnek el az egyes ütközések között?</wlatex><includeonly><wlatex>{{Végeredmény|content=A keresett időközök $0,37\,\rm s$ és $0,08\,\rm s$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># (3.3.17.) A vízszintessel $30^{\circ}$-os szöget képező $5\,\rm m$ magasságú lejtőn egyidejűleg kezdősebesség nélkül elindítunk egy hasábot, egy hengert és egy golyót. A hasáb súrlódásmentesen csúszik, a henger és a golyó csúszásmentesen gördül. A testek különböző időtartamok alatt érnek a lejtő aljára, ahol lécbe ütköznek. Mekkora időközök telnek el az egyes ütközések között?</wlatex><includeonly><wlatex>{{Végeredmény|content=A keresett időközök $0,37\,\rm s$ és $0,08\,\rm s$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A hasáb gyorsulása $$a_1=g\sin{\alpha}=\frac g2,$$ homogén tömör hengert feltételezve annak gyorsulása $$a_2=\frac23g\sin{\alpha}=\frac g3$$ | + | <wlatex>A hasáb gyorsulása $$a_1=g\sin{\alpha}=\frac g2,$$ homogén tömör hengert feltételezve annak gyorsulása az előző feladat mintájára $$a_2=\frac23g\sin{\alpha}=\frac g3.$$ A homogén tömör gömb tehetetlenségi nyomatéka $\theta=\frac25mR^2$, ezzel a gyorsulása $$a_3=\frac57g\sin{\alpha}=0,36g$$ Mivel $a_1>a_3>a_2$, először a hasáb, majd a gömb, végül a henger érkezik le $t=\sqrt{\frac{2s}a}$ idő alatt, ahol $s=\frac h{\sin{\alpha}}=10\,\rm m$-re jön ki. A leérkezés ideje rendre $2,02\,\rm s$, $2,47\,\rm s$ és $2,39\,\rm s$, így a keresett időközök $0,37\,\rm s$ és $0,08\,\rm s$.</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 26., 13:23-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (3.3.17.) A vízszintessel
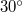-os szöget képező 
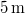magasságú lejtőn egyidejűleg kezdősebesség nélkül elindítunk egy hasábot, egy hengert és egy golyót. A hasáb súrlódásmentesen csúszik, a henger és a golyó csúszásmentesen gördül. A testek különböző időtartamok alatt érnek a lejtő aljára, ahol lécbe ütköznek. Mekkora időközök telnek el az egyes ütközések között?
Megoldás
A hasáb gyorsulása![\[a_1=g\sin{\alpha}=\frac g2,\]](/images/math/2/f/2/2f2b80f0e2a0bb871484ca5a9fd47068.png)
![\[a_2=\frac23g\sin{\alpha}=\frac g3.\]](/images/math/a/a/8/aa81dbc3f954a4c672aff9273d5bd10a.png)
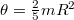, ezzel a gyorsulása ![\[a_3=\frac57g\sin{\alpha}=0,36g\]](/images/math/f/9/1/f9132fff6fa3d4b726ed6ecb17ae7f56.png)
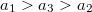, először a hasáb, majd a gömb, végül a henger érkezik le 
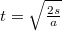idő alatt, ahol 
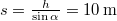-re jön ki. A leérkezés ideje rendre 
, 
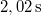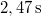és 
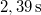, így a keresett időközök 
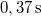és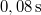 
.
