„Elektrosztatika példák - Kétrétegű dielektrikummal töltött síkkondenzátor” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Egy síkkondenzátor dielektrikuma két rétegből áll, amelyek elválasztó felülete a fegyverzetekkel párhuzamos. Meghatározandó a kondenzátorra kapcsolható legnagyobb feszültség, ha az egyik réteg vastagsága $d_{1}$, relatív permittivitása $\epsilon_{1}$, és átütési szilárdsága $E_{kr1}$. Ugyanezek az értékek a másik rétegre: $d_{2},\epsilon_{2},E_{kr2}$. | </noinclude><wlatex># Egy síkkondenzátor dielektrikuma két rétegből áll, amelyek elválasztó felülete a fegyverzetekkel párhuzamos. Meghatározandó a kondenzátorra kapcsolható legnagyobb feszültség, ha az egyik réteg vastagsága $d_{1}$, relatív permittivitása $\epsilon_{1}$, és átütési szilárdsága $E_{kr1}$. Ugyanezek az értékek a másik rétegre: $d_{2},\epsilon_{2},E_{kr2}$. | ||
| − | </wlatex><includeonly><wlatex> | + | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$U = \frac{E_{kr}}{\epsilon_1} \cdot d_1 + \frac{E_{kr}}{\epsilon_2} \cdot d_2$$ <br> ahol $$E_{kr} = \min\left\lbrace E_{kr1},E_{kr2}\right\rbrace $$}} |
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| − | A Gauss-tételből következik, hogy a kondenzátorban jelenlévő elektromos eltolás | + | A Gauss-tételből következik, hogy a kondenzátorban jelenlévő elektromos eltolás nagysága mindkét közegben: $D = \omega$, ahol $\omega$ a kondenzátor fegyverzeteire felvitt szabad töltés. |
| − | Ebből következik, hogy az elektromos térerősség a két térrészben: | + | Ebből következik, hogy az elektromos térerősség nagysága a két térrészben: |
| − | $$ | + | $$E_1 = \frac{\omega}{\epsilon_0\cdot\epsilon_1}$$ |
| − | $$ | + | $$E_2 = \frac{\omega}{\epsilon_0\cdot\epsilon_2}$$ |
Ezekkel, a két fegyverzet között fellépő potenciálkülönbség: | Ezekkel, a két fegyverzet között fellépő potenciálkülönbség: | ||
$$U = E_1\cdot d_1 + E_2\cdot d_2$$ | $$U = E_1\cdot d_1 + E_2\cdot d_2$$ | ||
A lap jelenlegi, 2013. szeptember 13., 17:50-kori változata
Feladat
- Egy síkkondenzátor dielektrikuma két rétegből áll, amelyek elválasztó felülete a fegyverzetekkel párhuzamos. Meghatározandó a kondenzátorra kapcsolható legnagyobb feszültség, ha az egyik réteg vastagsága
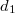, relatív permittivitása 
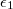, és átütési szilárdsága 
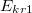. Ugyanezek az értékek a másik rétegre: 
.
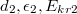Megoldás
A Gauss-tételből következik, hogy a kondenzátorban jelenlévő elektromos eltolás nagysága mindkét közegben: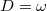 
, ahol 
a kondenzátor fegyverzeteire felvitt szabad töltés.
Ebből következik, hogy az elektromos térerősség nagysága a két térrészben:
![\[E_1 = \frac{\omega}{\epsilon_0\cdot\epsilon_1}\]](/images/math/4/8/e/48e38f6ba736bd17c900090485a99dd0.png)
![\[E_2 = \frac{\omega}{\epsilon_0\cdot\epsilon_2}\]](/images/math/1/2/0/120afdf1d9e2e08fe39296dab618336b.png)
Ezekkel, a két fegyverzet között fellépő potenciálkülönbség:
![\[U = E_1\cdot d_1 + E_2\cdot d_2\]](/images/math/b/7/5/b75d0039883b417d4480d0b9fea007ad.png)
A fegyverzetek közé kapcsolható maximális potenciálkülönbség pedig:
![\[U = \frac{E_{kr}}{\epsilon_1} \cdot d_1 + \frac{E_{kr}}{\epsilon_2} \cdot d_2\]](/images/math/f/0/f/f0f7bb833f291f4e0429052e23cb9a23.png)
![\[E_{kr} = \min\left\lbrace E_{kr1},E_{kr2}\right\rbrace \]](/images/math/6/5/8/658366583dd75fb4986ba28072f9bb00.png)
