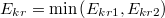„Elektrosztatika példák - Szigetelővel töltött hengerkondenzátor” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| (egy szerkesztő 5 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
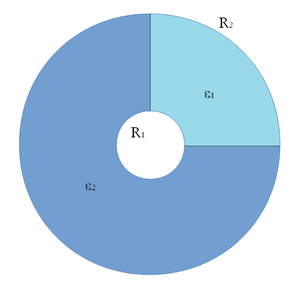
| − | </noinclude><wlatex>#Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara $R_1$ és $R_2$, | + | </noinclude><wlatex>#Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara $R_1$ és $R_2$, $h$ hosszúságú szakaszon a töltésük $+Q$ és$-Q$. A szigetelők relatív permittivitása $\epsilon_1$ és $\epsilon_2$. <br> '''a)''' Írja fel az $\vec{E}$ térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben! <br> '''b)''' Írja fel a $\vec{D}$ elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben! <br> '''c)''' Határozza meg a $h$ hosszúságú szakasz kapacitását! <br> '''d)''' Mekkora lehet a $Q$ töltés, ha kondenzátorban használt szigetelő anyagok ($E_{kr1}$ illetve $E_{kr2}$) kritikus felett átütnek, és elveszítik szigetelő tulajdonságukat? <br> [[Kép:KFGY2-3-6.png|none|300px]] |
</wlatex><includeonly><wlatex>{{Végeredmény|content='''a)''' $$\vec{E} = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) $$ <br> '''b)''' $$\vec{D_1} = \epsilon_1\cdot\vec{E} = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ $$\vec{D_2} = \epsilon_2\cdot\vec{E} = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ <br> '''c)''' $$C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}$$'''d)''' $$Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)$$ <br> ahol $E_{kr} = \min\left(E_{kr1},E_{kr2}\right)$}} | </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)''' $$\vec{E} = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) $$ <br> '''b)''' $$\vec{D_1} = \epsilon_1\cdot\vec{E} = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ $$\vec{D_2} = \epsilon_2\cdot\vec{E} = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ <br> '''c)''' $$C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}$$'''d)''' $$Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)$$ <br> ahol $E_{kr} = \min\left(E_{kr1},E_{kr2}\right)$}} | ||
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| − | a, Írjuk fel a Gauss-tételt egy $ | + | a, Írjuk fel a Gauss-tételt egy $l$ hosszúságú, $r$ sugarú, a fegyverzetekkel koncentrikusan elhelyezkedő hengerfelületre. |
$$\int \vec{D}\cdot\vec{dA} = Q$$ | $$\int \vec{D}\cdot\vec{dA} = Q$$ | ||
| − | + | Az $r$ sugarú felületen az elektromos tér sugárirányú komponensének nagysága szükségszerűen megegyezik a két közegben, máskülönben az egyes fémhengerek nem lennének ekvipotenciális felületek. Ugyanazon $E$ elektromos térhez azonban két eltérő elektromos eltolás érték tartozik az eltérő dielektromos állandójú közegekben. | |
| − | $$ | + | |
| − | $$2\pi r l\cdot\left(\frac{ | + | $$D_1\frac{1}{4} 2\pi r l +D_2\frac{3}{4} 2 \pi r l = Q$$ |
| − | + | ||
| − | $$2\pi r l \left(\frac{\epsilon_0\epsilon_1\cdot | + | $$2\pi r l\cdot\left(\frac{D_1}{4}+\frac{3\cdot D_2}{4}\right) = Q$$ |
| − | $$ | + | |
| + | Alkalmazva az elektromos eltolás és az elektromos tér közti $E=\epsilon D$ összefüggést: | ||
| + | |||
| + | $$2\pi r l \left(\frac{\epsilon_0\epsilon_1\cdot E}{4}+\frac{\epsilon_0\epsilon_2\cdot 3\cdot E}{4}\right) = Q$$ | ||
| + | |||
| + | Az egyenletből kifejezve a térerősséget: | ||
| + | |||
| + | $$E = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) $$ | ||
b, Az előző rész eredményeit felhasználva az elektromos eltolás a két közegben: | b, Az előző rész eredményeit felhasználva az elektromos eltolás a két közegben: | ||
| − | $$ | + | $$D_1 = \epsilon_1\cdot E = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ |
| − | $$ | + | $$D_2 = \epsilon_2\cdot E = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ |
c, A fegyverzetek közötti potenciálkülönbség: | c, A fegyverzetek közötti potenciálkülönbség: | ||
$$U = \int_{R1}^{R_2}\vec{E}\cdot\vec{dr} = \frac{2Q}{\pi l \epsilon_0}\cdot\left(\frac{1}{\epsilon_1+3\epsilon_2} \right)\cdot\ln\left(\frac{R_2}{R_1}\right) $$ | $$U = \int_{R1}^{R_2}\vec{E}\cdot\vec{dr} = \frac{2Q}{\pi l \epsilon_0}\cdot\left(\frac{1}{\epsilon_1+3\epsilon_2} \right)\cdot\ln\left(\frac{R_2}{R_1}\right) $$ | ||
| − | Ebből a | + | Ebből a kapacitás: |
$$C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}$$ | $$C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}$$ | ||
d, A kondenzátor akkor üt át, ha a kilakuló legnagyobb térerősség, nagyobb, mint a kritikus térerősség. A legnagyobb tér a kondenzátorban a belső hengerfelületen van, ezért a felvihető legnagyobb töltés: | d, A kondenzátor akkor üt át, ha a kilakuló legnagyobb térerősség, nagyobb, mint a kritikus térerősség. A legnagyobb tér a kondenzátorban a belső hengerfelületen van, ezért a felvihető legnagyobb töltés: | ||
A lap jelenlegi, 2013. szeptember 14., 19:54-kori változata
Feladat
- Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara
és 
, 
hosszúságú szakaszon a töltésük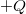 
és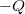
. A szigetelők relatív permittivitása 
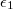és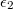 
.
a) Írja fel az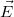
térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
b) Írja fel a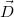
elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
c) Határozza meg a hosszúságú szakasz kapacitását!
d) Mekkora lehet a
töltés, ha kondenzátorban használt szigetelő anyagok (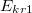
illetve 
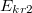) kritikus felett átütnek, és elveszítik szigetelő tulajdonságukat?
Megoldás
a, Írjuk fel a Gauss-tételt egy 
hosszúságú, 
sugarú, a fegyverzetekkel koncentrikusan elhelyezkedő hengerfelületre.
![\[\int \vec{D}\cdot\vec{dA} = Q\]](/images/math/e/2/f/e2fb0baf4ee65ef1dce66b07241ba551.png)
Az sugarú felületen az elektromos tér sugárirányú komponensének nagysága szükségszerűen megegyezik a két közegben, máskülönben az egyes fémhengerek nem lennének ekvipotenciális felületek. Ugyanazon 
elektromos térhez azonban két eltérő elektromos eltolás érték tartozik az eltérő dielektromos állandójú közegekben.
![\[D_1\frac{1}{4} 2\pi r l +D_2\frac{3}{4} 2 \pi r l = Q\]](/images/math/6/f/5/6f5c67cccddb7b85bd37f4c22a81a9f8.png)
![\[2\pi r l\cdot\left(\frac{D_1}{4}+\frac{3\cdot D_2}{4}\right) = Q\]](/images/math/b/d/6/bd61d676804d5ac26d98453896e5861c.png)
Alkalmazva az elektromos eltolás és az elektromos tér közti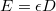 
összefüggést:
![\[2\pi r l \left(\frac{\epsilon_0\epsilon_1\cdot E}{4}+\frac{\epsilon_0\epsilon_2\cdot 3\cdot E}{4}\right) = Q\]](/images/math/b/e/6/be6c0644f8346e8b36a45e3f74eec45f.png)
Az egyenletből kifejezve a térerősséget:
![\[E = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) \]](/images/math/e/a/2/ea2fe83445ec86489eceb3cdee58c107.png)
b, Az előző rész eredményeit felhasználva az elektromos eltolás a két közegben:
![\[D_1 = \epsilon_1\cdot E = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)\]](/images/math/0/1/8/018f7e506ce6611873b42ad14a478a34.png)
![\[D_2 = \epsilon_2\cdot E = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)\]](/images/math/3/3/3/333f0a079e8ca412fbdaa55d28af59fc.png)
c, A fegyverzetek közötti potenciálkülönbség:
![\[U = \int_{R1}^{R_2}\vec{E}\cdot\vec{dr} = \frac{2Q}{\pi l \epsilon_0}\cdot\left(\frac{1}{\epsilon_1+3\epsilon_2} \right)\cdot\ln\left(\frac{R_2}{R_1}\right) \]](/images/math/f/6/2/f62e80f038420237bd718fba85802c32.png)
Ebből a kapacitás:
![\[C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}\]](/images/math/d/9/f/d9f9666b26fd1fc99847d2cfa664a918.png)
d, A kondenzátor akkor üt át, ha a kilakuló legnagyobb térerősség, nagyobb, mint a kritikus térerősség. A legnagyobb tér a kondenzátorban a belső hengerfelületen van, ezért a felvihető legnagyobb töltés:
![\[Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)\]](/images/math/7/5/6/7568cc9135352f16688c33daad9d0fe6.png)
Ahol 
