„Elektrosztatika példák - Dielektriumba helyezett fémgömb potenciáltere” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Megoldás) |
||
| 18. sor: | 18. sor: | ||
Ha $r<R_1$, akkor $\vec{D} = 0$ és $\vec{E} = 0$, hiszen az integrálási tartományon belül nem található töltés. | Ha $r<R_1$, akkor $\vec{D} = 0$ és $\vec{E} = 0$, hiszen az integrálási tartományon belül nem található töltés. | ||
Ha $r>R_1$, akkor az elektromos eltolás nagysága a következő: | Ha $r>R_1$, akkor az elektromos eltolás nagysága a következő: | ||
| − | $$D\cdot 4\cdot\pi\cdot r = Q \Rightarrow D = \frac{Q}{4\cdot\pi\cdot r^2}$$ | + | $$D\cdot 4\cdot\pi\cdot r^2 = Q \Rightarrow D = \frac{Q}{4\cdot\pi\cdot r^2}$$ |
Az ebből származtatható elektromos tér nagysága pedig függ a gömböt koncentrikusan körülvevő anyag dielektromos állandójától: $$E = \frac{D}{\epsilon_0\cdot\epsilon_r}$$. | Az ebből származtatható elektromos tér nagysága pedig függ a gömböt koncentrikusan körülvevő anyag dielektromos állandójától: $$E = \frac{D}{\epsilon_0\cdot\epsilon_r}$$. | ||
A lap 2013. szeptember 27., 13:03-kori változata
Feladat
- Egy
sugarú, 
térfogati töltéssűrűséggel egyenletesen töltött gömböt egy 
vastagságú,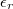 
permittivitásű szigetelővel veszünk körbe. Hogyan függ a potenciál a centrumtól mért távolságtól?
Megoldás
Legyen a külső gömb sugara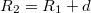 
, töltése pedig 
. Írjuk fel a Gauss-tételt egy 
sugarú gömbre, amely koncentrikus -el és 
-vel.
![\[\int \int\vec{D}\cdot{\vec{dA}} = Q\]](/images/math/5/4/5/5454396302db853cf92b15f4e64c2208.png)
Ha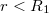 
, akkor 
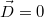és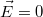 
, hiszen az integrálási tartományon belül nem található töltés.
Ha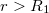 
, akkor az elektromos eltolás nagysága a következő:
![\[D\cdot 4\cdot\pi\cdot r^2 = Q \Rightarrow D = \frac{Q}{4\cdot\pi\cdot r^2}\]](/images/math/6/6/6/6660301c53247ded06e57d9bc441d25e.png)
![\[E = \frac{D}{\epsilon_0\cdot\epsilon_r}\]](/images/math/9/0/9/909d6397f061cbf47fcc772943c0c37e.png)
Így az elektromos tér a dielektrikum rétegben (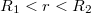
):
![\[E = \frac{Q}{4\cdot\pi\cdot r^2\cdot\epsilon_0\cdot\epsilon_r}\]](/images/math/3/1/9/319b7dca9fe4391208a51aefc800d65a.png)
A dielektrikum rétegen kívül (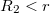
) :
![\[E = \frac{Q}{4\cdot\pi\cdot r^2\cdot\epsilon_0}\]](/images/math/c/b/2/cb22650fa44a9c28ccb7f4eddc0e26c0.png)
A potenciált az függvényében a következő integrál adja meg:
![\[U\left(r\right) = -\int_\infty^r E\left(\tilde{r}\right)\cdot d\tilde{r}\]](/images/math/b/6/6/b661043d7f9bef946c0d299f00c3f46e.png)
A dielektrikum rétegen kívül: ()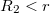
![\[U = \frac{Q}{4\cdot\pi\cdot r\cdot\epsilon_0\cdot}\]](/images/math/a/f/0/af0807207b916b59efa499876d00de24.png)
A dielektrikumban: ()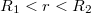
![\[U = \frac{Q}{4\cdot\pi\cdot R_2\cdot\epsilon_0\cdot}+\frac{Q}{4\cdot\pi\cdot\epsilon_0\cdot\epsilon_r}\cdot\left(\frac{1}{r}-\frac{1}{R_2}\right)\]](/images/math/4/2/f/42fea07df3ecaebb14ec25042ea7bf1d.png)
A fémgömb belsejében a potenciál konstans, hiszen ott nincs elektromos tér. A potenciál értéke:
![\[U = \frac{Q}{4\cdot\pi\cdot R_2\cdot\epsilon_0\cdot}+\frac{Q}{4\cdot\pi\cdot\epsilon_0\cdot\epsilon_r}\cdot\left(\frac{1}{R_1}-\frac{1}{R_2}\right) \]](/images/math/c/3/a/c3a22f84c1c1c89b99eaa62167b22f14.png)
