„Elektrosztatika - Kapacitás, kondenzátorok. Elrendezések energiája” változatai közötti eltérés
A Fizipedia wikiből
| 10. sor: | 10. sor: | ||
{{:Elektrosztatika példák - R sugarú fémgömb kapacitása}}{{Megoldás|link=Elektrosztatika példák - R sugarú fémgömb kapacitása}} | {{:Elektrosztatika példák - R sugarú fémgömb kapacitása}}{{Megoldás|link=Elektrosztatika példák - R sugarú fémgömb kapacitása}} | ||
{{:Elektrosztatika példák - Hengerkondenzátor kapacitása}}{{Megoldás|link=Elektrosztatika példák - Hengerkondenzátor kapacitása}} | {{:Elektrosztatika példák - Hengerkondenzátor kapacitása}}{{Megoldás|link=Elektrosztatika példák - Hengerkondenzátor kapacitása}} | ||
| − | {{:Elektrosztatika példák - Párhuzamos hengeres vezetékek kapacitása}}{{Megoldás|link=Párhuzamos hengeres vezetékek kapacitása}} | + | {{:Elektrosztatika példák - Párhuzamos hengeres vezetékek kapacitása}}{{Megoldás|link=Elektrosztatika példák - Párhuzamos hengeres vezetékek kapacitása}} |
{{:Elektrosztatika példák - Hengeres vezetékből és végtelen vezető síkból álló rendszer kapacitása}}{{Megoldás|link=Elektrosztatika példák - Hengeres vezetékből és végtelen vezető síkból álló rendszer kapacitása}} | {{:Elektrosztatika példák - Hengeres vezetékből és végtelen vezető síkból álló rendszer kapacitása}}{{Megoldás|link=Elektrosztatika példák - Hengeres vezetékből és végtelen vezető síkból álló rendszer kapacitása}} | ||
{{:Elektrosztatika példák - Két azonos sugarú fémgömbből álló rendszer kapacitása}}{{Megoldás|link=Elektrosztatika példák - Két azonos sugarú fémgömbből álló rendszer kapacitása}} | {{:Elektrosztatika példák - Két azonos sugarú fémgömbből álló rendszer kapacitása}}{{Megoldás|link=Elektrosztatika példák - Két azonos sugarú fémgömbből álló rendszer kapacitása}} | ||
A lap jelenlegi, 2013. július 1., 18:30-kori változata
Feladatok
- Számítsuk ki az
 ,
,  sugarakkal adott gömbkondenzátor kapacitását, ha a fegyverzetek között levegő van.
sugarakkal adott gömbkondenzátor kapacitását, ha a fegyverzetek között levegő van.
- Mekkora egy
 sugarú fémgömb kapacitása?
sugarú fémgömb kapacitása?
- Számítsuk ki egy
 hosszúságú,
hosszúságú, 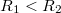 sugarakkal rendelkező hengerkondenzátor kapacitását, ha a hengerek között levegő van. Legyen
sugarakkal rendelkező hengerkondenzátor kapacitását, ha a hengerek között levegő van. Legyen 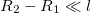 , azaz tekintsünk el a kondenzátor végein kialakuló szórt tértől!
, azaz tekintsünk el a kondenzátor végein kialakuló szórt tértől!
- Két azonos,
 keresztmetszeti sugarú,
keresztmetszeti sugarú,  hosszúságú hengeres vezeték fekszik egymás mellett párhuzamosan, egymástól
hosszúságú hengeres vezeték fekszik egymás mellett párhuzamosan, egymástól 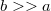 távolságra. Mekkora a rendszer kapacitása? (
távolságra. Mekkora a rendszer kapacitása? (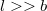 )
)
 hosszúságú egyenes hengeres vezeték párhuzamosan helyezkedik el egy végtelen vezető síkkal. A vezeték keresztmetszetének sugara
hosszúságú egyenes hengeres vezeték párhuzamosan helyezkedik el egy végtelen vezető síkkal. A vezeték keresztmetszetének sugara  , a távolság a vezeték síkhoz legközelebbi pontja és a sík között
, a távolság a vezeték síkhoz legközelebbi pontja és a sík között  . Mekkora a rendszer kapacitása? (
. Mekkora a rendszer kapacitása? (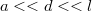 )
)
- Mekkora két azonos ,
 sugarú fémgömbből álló rendszer kapacitása, ha gömbök felületének egymáshoz legközelebbi pontjai
sugarú fémgömbből álló rendszer kapacitása, ha gömbök felületének egymáshoz legközelebbi pontjai  távolságra helyezkednek el? (
távolságra helyezkednek el? (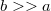 )
)
- Mekkora annak a rendszernek a kapacitása, amely egy
 sugarú fémgömbből, valamint ennek középpontjától
sugarú fémgömbből, valamint ennek középpontjától  távolságra elhelyezett végtelen vezető síkból áll? (
távolságra elhelyezett végtelen vezető síkból áll? (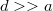 )
)
- Síkkondenzátor
 területű lemezei között levegő van. Mennyi munkát kell végezni ahhoz, hogy a lemezek közötti távolságot lassan
területű lemezei között levegő van. Mennyi munkát kell végezni ahhoz, hogy a lemezek közötti távolságot lassan 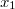 -ről
-ről 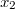 -re növeljük, ha a folyamat során
-re növeljük, ha a folyamat során
a) a lemezekre vitt töltést;
töltést;
b) a lemezek közötti feszültséget tartjuk állandónak?
feszültséget tartjuk állandónak?
- Egy
 sugarú gömbben homogén
sugarú gömbben homogén  térfogati töltéssűrűség van. Határozzuk meg az elrendezés energiáját!
térfogati töltéssűrűség van. Határozzuk meg az elrendezés energiáját!
 távolság függvényében
távolság függvényében ![\[C=\dfrac{Q}{U_{1,2}}=\dfrac{4\pi\varepsilon_0}{\left( \dfrac{1}{R_1}-\dfrac{1}{R_2} \right)}\]](/images/math/f/f/b/ffbeac6e74b837a6a77e3415207a2c39.png)
![\[C=\dfrac{Q}{U}=4\pi\varepsilon_0 R\]](/images/math/7/7/f/77fb8c0d085dcb05c2e22b2ed5c45b17.png)
![\[C=\dfrac{2\pi l \varepsilon_0}{ln \left( \dfrac{R_2}{R_1} \right)}\]](/images/math/e/0/4/e0423b95b55b6b553575115250e0f1b6.png)
![\[C=\dfrac{Q}{U_{AB}}=\dfrac{Q=2\pi a l \omega}{\dfrac{2\omega a}{\varepsilon_0} ln \left( \dfrac{b-a}{a} \right)}=\dfrac{\pi l \varepsilon_0}{ln \left( \dfrac{b-a}{a} \right)}\]](/images/math/0/c/3/0c32ac863e4b3b202ac8f4a34725cbf6.png)
![\[C=2C^*=\dfrac{2 \pi l \varepsilon_0}{ln \left( \dfrac{2d-a}{a} \right)}\]](/images/math/8/f/2/8f2410ff0287890c12e2461388e1e97e.png)
![\[C=\dfrac{Q}{U_{AB}}=\dfrac{2\pi \varepsilon_0}{\left( \dfrac{1}{a}-\dfrac{1}{b-a} \right)}\]](/images/math/1/b/5/1b5f85a731b3f5262b3bfd62789112a1.png)
![\[C=2C^*=\dfrac{4\pi \varepsilon_0}{\left( \dfrac{1}{a}-\dfrac{1}{2d-a} \right)}\]](/images/math/c/6/5/c65351ef90fc2960fc6d7842cc0a4c02.png)
![\[W=-W_{eroter}=\dfrac{q^2}{2S\varepsilon_0}(x_2-x_1)\]](/images/math/d/8/a/d8af3f1478b61c97dea5be6ece8d3d1f.png)
![\[W=-W_{eroter}=\dfrac{\varepsilon_0 U^2 S}{2} \left( \dfrac{1}{x_1}-\dfrac{1}{x_2} \right)\]](/images/math/c/f/2/cf2cf313570b69799160c5967489a55c.png)
![\[W=\dfrac{4 \rho^2 \pi R^5}{15 \varepsilon_0}\]](/images/math/4/c/9/4c9cb38d1d2f29cddb52eb3204968e09.png)