„Elektrosztatika példák - Fémlappal töltött síkkondenzátor” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Ideális síkkondenzátor fegyverzetei egymástól $d$ távolságra vannak. A kondenzátor beljesében a térerősség $E_0$. <br> '''a)''' Hányszorosára változik meg a kondenzátor kapacitása, ha a fegyverzetekkel párhuzamosan egy $\delta d$ | + | </noinclude><wlatex># Ideális síkkondenzátor fegyverzetei egymástól $d$ távolságra vannak. A kondenzátor beljesében a térerősség $E_0$. <br> '''a)''' Hányszorosára változik meg a kondenzátor kapacitása, ha a fegyverzetekkel párhuzamosan egy $\delta d$ vastagságú fémlemezt helyezünk a kondenzátor belsejébe? <br> '''b)''' Rajzolja fel a térerősséget, mint a fegyverzettől mért távolság függvényét, ha a fémlemezt a baloldali fegyverzettől $d_0$ távolságra van. <br> '''c)''' Rajzolja fel a potenciál változását a hely függvényében az előző összeállításnál! Mekkora a fegyverzetek közötti feszültség? <br> '''d)''' Milyen vastag a szigetelőlemez hatására változik a síkkondenzátor kapacitása ugyanannyiszorosára, mint a fémlemez esetében, ha $\epsilon_r$ adott? |
</wlatex><includeonly><wlatex>{{Végeredmény|content='''a)''' $$\frac{C_1}{C_0} = \frac{\frac{Q}{U_1}}{\frac{Q}{U_0}} = \frac{U_0}{U_1} = \frac{d}{d-\delta d}$$ <br> '''b)''' A térerősség a kondenzátorban konstans $E_0$, kivéve a fémben, ahol zérus. <br> '''c)''' A pontenciál a fegyverzetek között lineárisan növekszik, kivéve a fémben, ahol konstans értéket vesz fel. <br> '''d)''' $$U_2 = E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right)$$}} | </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)''' $$\frac{C_1}{C_0} = \frac{\frac{Q}{U_1}}{\frac{Q}{U_0}} = \frac{U_0}{U_1} = \frac{d}{d-\delta d}$$ <br> '''b)''' A térerősség a kondenzátorban konstans $E_0$, kivéve a fémben, ahol zérus. <br> '''c)''' A pontenciál a fegyverzetek között lineárisan növekszik, kivéve a fémben, ahol konstans értéket vesz fel. <br> '''d)''' $$U_2 = E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right)$$}} | ||
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| 19. sor: | 20. sor: | ||
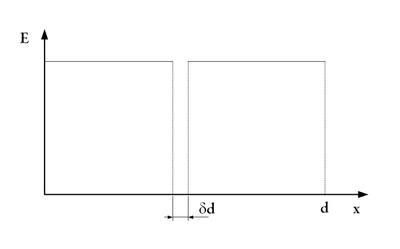
b, A térerősség a kondenzátorban konstans $E_0$, kivéve a fémben, ahol zérus. | b, A térerősség a kondenzátorban konstans $E_0$, kivéve a fémben, ahol zérus. | ||
[[Kép:KFGY2-3-2B.png|none|400px]] | [[Kép:KFGY2-3-2B.png|none|400px]] | ||
| − | |||
<br> | <br> | ||
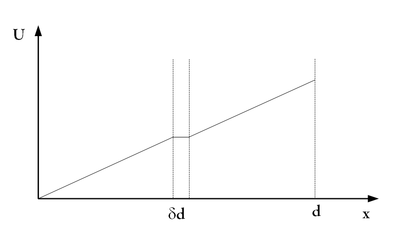
c, A pontenciál a fegyverzetek között lineárisan növekszik, kivéve a fémben, ahol konstans értéket vesz fel. | c, A pontenciál a fegyverzetek között lineárisan növekszik, kivéve a fémben, ahol konstans értéket vesz fel. | ||
[[Kép:KFGY2-3-2C.png|none|400px]] | [[Kép:KFGY2-3-2C.png|none|400px]] | ||
| − | |||
<br> | <br> | ||
| − | d, A szigetelő lemez vastagsága legyen:$\delta d_2$. A szigetelő lemezben a tér lecsökken | + | d, A szigetelő lemez vastagsága legyen:$\delta d_2$. A szigetelő lemezben a tér lecsökken, nagysága $\frac{E_0}{\epsilon_r}$ lesz. Ezért a lemezek közötti potenciálkülönbség értéke: |
$$U_2 = E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right)$$ | $$U_2 = E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right)$$ | ||
| − | Mivel a fegyverzeteken a töltés mind a két esetben állandó, ezért a két | + | Mivel a fegyverzeteken a töltés mind a két esetben állandó, ezért a két elrendezés kapacitása akkor fog megegyezni, ha lemezek közötti potenciálkülönbség megegyezik. Vagyis, ha: |
$$U_2 = U_1$$ | $$U_2 = U_1$$ | ||
$$E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right) = E_0\cdot\left(d-\delta d\right)$$ | $$E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right) = E_0\cdot\left(d-\delta d\right)$$ | ||
| − | Amiből | + | Amiből kifejezhető a szükséges vastagság: |
$$\delta d_2 = \frac{\delta d}{1-\frac{1}{\epsilon_r}}$$ | $$\delta d_2 = \frac{\delta d}{1-\frac{1}{\epsilon_r}}$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. szeptember 13., 17:56-kori változata
Feladat
- Ideális síkkondenzátor fegyverzetei egymástól
távolságra vannak. A kondenzátor beljesében a térerősség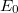 
.
a) Hányszorosára változik meg a kondenzátor kapacitása, ha a fegyverzetekkel párhuzamosan egy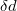
vastagságú fémlemezt helyezünk a kondenzátor belsejébe?
b) Rajzolja fel a térerősséget, mint a fegyverzettől mért távolság függvényét, ha a fémlemezt a baloldali fegyverzettől
távolságra van.
c) Rajzolja fel a potenciál változását a hely függvényében az előző összeállításnál! Mekkora a fegyverzetek közötti feszültség?
d) Milyen vastag a szigetelőlemez hatására változik a síkkondenzátor kapacitása ugyanannyiszorosára, mint a fémlemez esetében, ha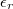
adott?
Megoldás
A fémben a térerősség értéke zérus, ezért a lemezek közötti potenciál a következő lesz:
![\[U = E_0\cdot\left(d-\delta d\right)\]](/images/math/c/6/1/c61341bc0241f3bbd60aa0fcf910536c.png)
a, Mivel a fegyverzeteken lévő töltés mennyisége nem változik meg, ezért a kapacitás megváltozása:
![\[\frac{C_1}{C_0} = \frac{\frac{Q}{U_1}}{\frac{Q}{U_0}} = \frac{U_0}{U_1} = \frac{d}{d-\delta d}\]](/images/math/d/f/6/df6ebefccd82ebee28c598d862fd6025.png)
b, A térerősség a kondenzátorban konstans 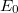, kivéve a fémben, ahol zérus.
c, A pontenciál a fegyverzetek között lineárisan növekszik, kivéve a fémben, ahol konstans értéket vesz fel.
d, A szigetelő lemez vastagsága legyen: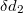
. A szigetelő lemezben a tér lecsökken, nagysága 
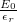lesz. Ezért a lemezek közötti potenciálkülönbség értéke:
![\[U_2 = E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right)\]](/images/math/5/c/7/5c734cf2918bce0aff495076d44f804f.png)
Mivel a fegyverzeteken a töltés mind a két esetben állandó, ezért a két elrendezés kapacitása akkor fog megegyezni, ha lemezek közötti potenciálkülönbség megegyezik. Vagyis, ha:
![\[U_2 = U_1\]](/images/math/6/7/a/67aeed8d4bdc4a649b1b7cb9c9019777.png)
![\[E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right) = E_0\cdot\left(d-\delta d\right)\]](/images/math/3/b/9/3b937d0d895e1a3b8540c085e18e824b.png)
Amiből kifejezhető a szükséges vastagság:
![\[\delta d_2 = \frac{\delta d}{1-\frac{1}{\epsilon_r}}\]](/images/math/7/e/1/7e1d95f40f1610aa941214f3bbdab311.png)
