„Mechanika - Lelógatott korong tárcsával és tömeggel” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
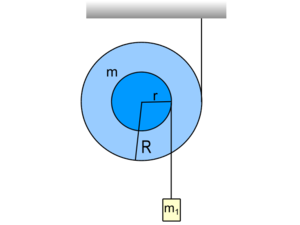
| − | </noinclude><wlatex># (*3.3.7.) $2R$ sugarú $4m$ tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű $R$ sugarú tárcsa kerületére csavart fonál végére $m$ tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását! | + | </noinclude><wlatex># (*3.3.7.) $2R$ sugarú $4m$ tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű $R$ sugarú tárcsa kerületére csavart fonál végére $m$ tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását! [[Kép:Kfgy1_3.3.7.svg|none|300px]]</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\beta=\frac{9g}{25R}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>Legyen a korong az 1-es test, az azt tartó kötélerő $K_1$, a másik test a 2-es, és a kettő közti kötélben ható erő $K_2$. A megadott adatokkal $\theta_{\rm{TKP}}=8mR^2$. A mozgásegyenletek mozgásirányban pozitív koordinátatengelyekkel $$ma_2=mg-K_2$$ $$4ma_1=4mg+K_2-K_1$$ $$\theta_{\rm{TKP}}\beta=8mR^2\cdot\frac{a_1}{2R}=K_1 2R-K_2R$$ Ez három egyenlet négy ismeretlenre (gyorulások és kötélerők), a még hiányzó egyenlet már csak a két test mozgásának viszonyáról szólhat: $$a_2=\frac{a_1}2$$ Ehhez úgy jutunk, ha megnézzük, mennyit változik a 2-es test magassága, ha $l_1$ hosszúságú kötél csavarodik le a korongról. Emiatt a test $l_1$-el lejjebb kerülne, de közben a tárcsán felcsavarodik $\frac{l_1}2$ hosszúságú kötél, emiatt ennyivel feljebb kerülne. Összességében tehát $l_2=l_1-\frac{l_1}2$ a magasságváltozás, ezt kétszer idő szerint deriválva kapjuk a gyorsulások viszonyát. Áttérve a szöggyorsulásra és $K_2$-t behelyettesítve már csak két ismeretlen és két egyenlet van. Célszerű a másik kötélerőtől megszabadulni az egyenletek megfelelő lineáris kombinációjával, így kapható a szöggyorsulásra $$\beta=\frac{9g}{25R}$$.</wlatex> | <wlatex>Legyen a korong az 1-es test, az azt tartó kötélerő $K_1$, a másik test a 2-es, és a kettő közti kötélben ható erő $K_2$. A megadott adatokkal $\theta_{\rm{TKP}}=8mR^2$. A mozgásegyenletek mozgásirányban pozitív koordinátatengelyekkel $$ma_2=mg-K_2$$ $$4ma_1=4mg+K_2-K_1$$ $$\theta_{\rm{TKP}}\beta=8mR^2\cdot\frac{a_1}{2R}=K_1 2R-K_2R$$ Ez három egyenlet négy ismeretlenre (gyorulások és kötélerők), a még hiányzó egyenlet már csak a két test mozgásának viszonyáról szólhat: $$a_2=\frac{a_1}2$$ Ehhez úgy jutunk, ha megnézzük, mennyit változik a 2-es test magassága, ha $l_1$ hosszúságú kötél csavarodik le a korongról. Emiatt a test $l_1$-el lejjebb kerülne, de közben a tárcsán felcsavarodik $\frac{l_1}2$ hosszúságú kötél, emiatt ennyivel feljebb kerülne. Összességében tehát $l_2=l_1-\frac{l_1}2$ a magasságváltozás, ezt kétszer idő szerint deriválva kapjuk a gyorsulások viszonyát. Áttérve a szöggyorsulásra és $K_2$-t behelyettesítve már csak két ismeretlen és két egyenlet van. Célszerű a másik kötélerőtől megszabadulni az egyenletek megfelelő lineáris kombinációjával, így kapható a szöggyorsulásra $$\beta=\frac{9g}{25R}$$.</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. július 1., 11:09-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*3.3.7.)
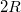 sugarú
sugarú 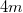 tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű
tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű  sugarú tárcsa kerületére csavart fonál végére
sugarú tárcsa kerületére csavart fonál végére  tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását!
tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását!
Megoldás
Legyen a korong az 1-es test, az azt tartó kötélerő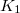 , a másik test a 2-es, és a kettő közti kötélben ható erő
, a másik test a 2-es, és a kettő közti kötélben ható erő 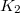 . A megadott adatokkal
. A megadott adatokkal 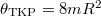 . A mozgásegyenletek mozgásirányban pozitív koordinátatengelyekkel
. A mozgásegyenletek mozgásirányban pozitív koordinátatengelyekkel ![\[ma_2=mg-K_2\]](/images/math/4/4/f/44fd22fda75c437123f446440acbe621.png)
![\[4ma_1=4mg+K_2-K_1\]](/images/math/f/3/b/f3b65d4c33c8deab3c7bdedb3f7f59f3.png)
![\[\theta_{\rm{TKP}}\beta=8mR^2\cdot\frac{a_1}{2R}=K_1 2R-K_2R\]](/images/math/8/3/5/83581c49faf484c0f706a6566fc647b6.png)
![\[a_2=\frac{a_1}2\]](/images/math/7/8/7/787cf75ac7298a281eda7e52b830f911.png)
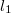 hosszúságú kötél csavarodik le a korongról. Emiatt a test
hosszúságú kötél csavarodik le a korongról. Emiatt a test 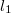 -el lejjebb kerülne, de közben a tárcsán felcsavarodik
-el lejjebb kerülne, de közben a tárcsán felcsavarodik 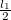 hosszúságú kötél, emiatt ennyivel feljebb kerülne. Összességében tehát
hosszúságú kötél, emiatt ennyivel feljebb kerülne. Összességében tehát 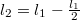 a magasságváltozás, ezt kétszer idő szerint deriválva kapjuk a gyorsulások viszonyát. Áttérve a szöggyorsulásra és
a magasságváltozás, ezt kétszer idő szerint deriválva kapjuk a gyorsulások viszonyát. Áttérve a szöggyorsulásra és 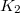 -t behelyettesítve már csak két ismeretlen és két egyenlet van. Célszerű a másik kötélerőtől megszabadulni az egyenletek megfelelő lineáris kombinációjával, így kapható a szöggyorsulásra
-t behelyettesítve már csak két ismeretlen és két egyenlet van. Célszerű a másik kötélerőtől megszabadulni az egyenletek megfelelő lineáris kombinációjával, így kapható a szöggyorsulásra ![\[\beta=\frac{9g}{25R}\]](/images/math/d/1/2/d12637c77eaf834854ae4d6e9937c236.png)