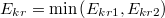„Elektrosztatika példák - Szigetelővel töltött hengerkondenzátor” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
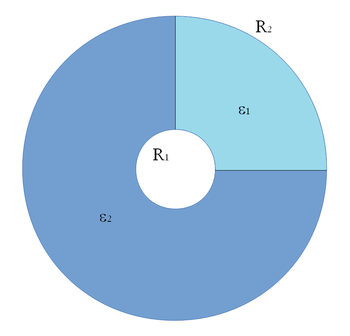
| − | </noinclude><wlatex>#Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara $R_1$ és $R_2$, és $h$ hosszúságú szakaszon a töltésük $+Q$ és$-Q$.A szigetelők relatív permittivitása $\epsilon_1$ és $\epsilon_2$. <br> '''a)''' Írja fel az $\vec{E}$ térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben! <br> '''b)''' Írja fel a $\vec{D}$ elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben! <br> '''c)''' Határozza meg a $h$ hosszúságú szakasz kapacitását! <br> '''d)''' Mekkora lehet a $Q$ töltés, ha kondenzátorban a szigetelő anyagok, a rájuk jellemző kritikus térerősség ($E_{kr1}$,$E_{kr2}$) felett átütnek, és elveszítik szigetelő tulajdonságukat? <br> | + | </noinclude><wlatex>#Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara $R_1$ és $R_2$, és $h$ hosszúságú szakaszon a töltésük $+Q$ és$-Q$.A szigetelők relatív permittivitása $\epsilon_1$ és $\epsilon_2$. <br> '''a)''' Írja fel az $\vec{E}$ térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben! <br> '''b)''' Írja fel a $\vec{D}$ elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben! <br> '''c)''' Határozza meg a $h$ hosszúságú szakasz kapacitását! <br> '''d)''' Mekkora lehet a $Q$ töltés, ha kondenzátorban a szigetelő anyagok, a rájuk jellemző kritikus térerősség ($E_{kr1}$,$E_{kr2}$) felett átütnek, és elveszítik szigetelő tulajdonságukat? <br> [[Kép:KFGY2-3-6.png|none|350px]] |
</wlatex><includeonly><wlatex>{{Végeredmény|content='''a)''' $$\vec{E} = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) $$ <br> '''b)''' $$\vec{D_1} = \epsilon_1\cdot\vec{E} = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ $$\vec{D_2} = \epsilon_2\cdot\vec{E} = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ <br> '''c)''' $$C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}$$'''d)''' $$Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)$$ <br> ahol $E_{kr} = \min\left(E_{kr1},E_{kr2}\right)$}} | </wlatex><includeonly><wlatex>{{Végeredmény|content='''a)''' $$\vec{E} = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) $$ <br> '''b)''' $$\vec{D_1} = \epsilon_1\cdot\vec{E} = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ $$\vec{D_2} = \epsilon_2\cdot\vec{E} = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)$$ <br> '''c)''' $$C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}$$'''d)''' $$Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)$$ <br> ahol $E_{kr} = \min\left(E_{kr1},E_{kr2}\right)$}} | ||
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
A lap 2013. július 28., 11:50-kori változata
Feladat
- Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara
és 
, és 
hosszúságú szakaszon a töltésük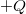 
és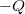
.A szigetelők relatív permittivitása 
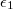és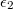 
.
a) Írja fel az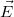
térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
b) Írja fel a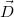
elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
c) Határozza meg a hosszúságú szakasz kapacitását!
d) Mekkora lehet a
töltés, ha kondenzátorban a szigetelő anyagok, a rájuk jellemző kritikus térerősség (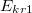
,
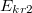) felett átütnek, és elveszítik szigetelő tulajdonságukat?
Megoldás
a, Írjuk fel a Gauss-tételt egy 
sugarú, 
hosszúságú , a fegyverzetekkel koncentrikus hengerre.
![\[\int \vec{D}\cdot\vec{dA} = Q\]](/images/math/e/2/f/e2fb0baf4ee65ef1dce66b07241ba551.png)
Mivel az elektromos eltolás más a két szigetelőben, ezért:
![\[\vec{D}_1\frac{1}{4} 2\pi r l +\vec{D}_2\frac{3}{4} 2 \pi r l = Q\]](/images/math/7/b/8/7b88397b3f4381014ea69efc37195ab7.png)
![\[2\pi r l\cdot\left(\frac{\vec{D}_1}{4}+\frac{3\cdot \vec{D}_2}{4}\right) = Q\]](/images/math/3/5/1/3515095089e846e683dac7f01046544a.png)
Mivel az elektromos térerősség tangenciális (sugár irányú) komponense folytonosan megy át a közeghatáron, ezért az, mindkét térrészben egyforma.
![\[2\pi r l \left(\frac{\epsilon_0\epsilon_1\cdot\vec{E}}{4}+\frac{\epsilon_0\epsilon_2\cdot 3\cdot \vec{E}}{4}\right) = Q\]](/images/math/5/d/2/5d29812170ad218cc16a42973ef04f18.png)
![\[\vec{E} = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) \]](/images/math/2/4/a/24a3abdf5a295a6cfbb2ec7f3835160e.png)
b, Az előző rész eredményeit felhasználva az elektromos eltolás a két közegben:
![\[\vec{D_1} = \epsilon_1\cdot\vec{E} = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)\]](/images/math/2/c/f/2cfbef7474bcbd37550e06bbd634d18e.png)
![\[\vec{D_2} = \epsilon_2\cdot\vec{E} = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)\]](/images/math/d/4/b/d4bc9a8ac76e4235127eb78c73b0ab1f.png)
c, A fegyverzetek közötti potenciálkülönbség:
![\[U = \int_{R1}^{R_2}\vec{E}\cdot\vec{dr} = \frac{2Q}{\pi l \epsilon_0}\cdot\left(\frac{1}{\epsilon_1+3\epsilon_2} \right)\cdot\ln\left(\frac{R_2}{R_1}\right) \]](/images/math/f/6/2/f62e80f038420237bd718fba85802c32.png)
Ebből a A kapacitás:
![\[C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}\]](/images/math/d/9/f/d9f9666b26fd1fc99847d2cfa664a918.png)
d, A kondenzátor akkor üt át, ha a kilakuló legnagyobb térerősség, nagyobb, mint a kritikus térerősség. A legnagyobb tér a kondenzátorban a belső hengerfelületen van, ezért a felvihető legnagyobb töltés:
![\[Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)\]](/images/math/7/5/6/7568cc9135352f16688c33daad9d0fe6.png)
Ahol 
