„Mechanika - Hokikorong és rúd ütközése” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 12. sor: | 12. sor: | ||
#: b) Mekkora lesz a tömegközéppont sebessége? | #: b) Mekkora lesz a tömegközéppont sebessége? | ||
#: c) Mekkora az e pontra vonatkoztatott tehetetlenségi nyomaték? | #: c) Mekkora az e pontra vonatkoztatott tehetetlenségi nyomaték? | ||
| − | #: d) Milyen szögsebességgel forog a rendszer ütközés után?</wlatex><includeonly><wlatex>{{Útmutatás|content=Merev testek tökéletesen rugalmatlan ütközésekor a két test "összetapad", és csak az impulzus meg az impulzusmomentum marad meg.}}{{Végeredmény|content= | + | #: d) Milyen szögsebességgel forog a rendszer ütközés után?</wlatex><includeonly><wlatex>{{Útmutatás|content=Merev testek tökéletesen rugalmatlan ütközésekor a két test "összetapad", és csak az impulzus meg az impulzusmomentum marad meg.}}{{Végeredmény|content=A rúd végétől $\frac l6$, a rúd tömegközéppontjától pedig $\frac l3$ $$v_{\rm{TKP}}=\frac23v_0$$ $$\theta=\frac{ml^2}4$$ $$\omega=\frac{4v_0}{3l}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>#: a) A tömegközéppont a rúdnak attól a végétől, ahol a koronggal összekapcsolódik, az $$x_{\rm{TKP}}3m=2m0+m\frac l2$$ egyenlet alapján $\frac l6$ távolságra, a rúd tömegközéppontjától pedig $\frac l3$ távolságra lesz. | <wlatex>#: a) A tömegközéppont a rúdnak attól a végétől, ahol a koronggal összekapcsolódik, az $$x_{\rm{TKP}}3m=2m0+m\frac l2$$ egyenlet alapján $\frac l6$ távolságra, a rúd tömegközéppontjától pedig $\frac l3$ távolságra lesz. | ||
| − | #: b) A rugalmatlan ütközés egyenlete a tömegközéppontra $2mv_0=3mv_{\rm{TKP}}$, ebből $$v_{\rm{TKP}}=\frac23v_0$$ | + | #: b) A rugalmatlan ütközés egyenlete a tömegközéppontra $2mv_0=3mv_{\rm{TKP}}$, ebből $$v_{\rm{TKP}}=\frac23v_0$$ |
#: c) A rúd tehetetlenségi nyomatéka a közös tömegközéppontra $$\theta_{\text{rúd}}=\frac{ml^2}{12}+m\left(\frac l3 \right)^2=\frac7{36}ml^2,$$ és ehhez jön még a korong $2m\left(\frac l6 \right)^2$ nyomatéka, így a teljes rendszer tehetetlenségi nyomatéka $\frac{ml^2}4$. | #: c) A rúd tehetetlenségi nyomatéka a közös tömegközéppontra $$\theta_{\text{rúd}}=\frac{ml^2}{12}+m\left(\frac l3 \right)^2=\frac7{36}ml^2,$$ és ehhez jön még a korong $2m\left(\frac l6 \right)^2$ nyomatéka, így a teljes rendszer tehetetlenségi nyomatéka $\frac{ml^2}4$. | ||
#: d) Az impulzusmomentum megmaradásból (a tömegközéppontra felírva) a szögsebesség $\omega=\frac{4v_0}{3l}$</wlatex> | #: d) Az impulzusmomentum megmaradásból (a tömegközéppontra felírva) a szögsebesség $\omega=\frac{4v_0}{3l}$</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2012. november 15., 15:01-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*3.3.24.) Egy pontszerűnek tekinthető
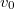sebességű 
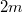tömegű hokikorong tökéletesen rugalmatlanul ütközik egy fele akkora tömegű, 
hosszúságú rúd végével (jégen). Írja le a rendszer mozgását ütközés után! ÁBRA
- a) Hol lesz az ütközés után a rendszer tömegközéppontja (a rúd hossza mentén)?
- b) Mekkora lesz a tömegközéppont sebessége?
- c) Mekkora az e pontra vonatkoztatott tehetetlenségi nyomaték?
- d) Milyen szögsebességgel forog a rendszer ütközés után?
Megoldás
- a) A tömegközéppont a rúdnak attól a végétől, ahol a koronggal összekapcsolódik, az egyenlet alapján
![\[x_{\rm{TKP}}3m=2m0+m\frac l2\]](/images/math/9/d/9/9d995805d24498d974dbc1489051c8b2.png)
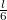távolságra, a rúd tömegközéppontjától pedig 
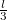távolságra lesz.
- b) A rugalmatlan ütközés egyenlete a tömegközéppontra
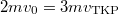, ebből ![\[v_{\rm{TKP}}=\frac23v_0\]](/images/math/5/d/5/5d5396ddab117439c0ca159e066f4fc2.png)
- c) A rúd tehetetlenségi nyomatéka a közös tömegközéppontra és ehhez jön még a korong
![\[\theta_{\text{rúd}}=\frac{ml^2}{12}+m\left(\frac l3 \right)^2=\frac7{36}ml^2,\]](/images/math/b/9/0/b909c0671defece563065f6d30a375b4.png)
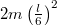nyomatéka, így a teljes rendszer tehetetlenségi nyomatéka 
.
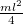- d) Az impulzusmomentum megmaradásból (a tömegközéppontra felírva) a szögsebesség
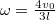
- a) A tömegközéppont a rúdnak attól a végétől, ahol a koronggal összekapcsolódik, az
