„Mechanika - Felbillenés lejtőn” változatai közötti eltérés

A lap 2013. szeptember 8., 18:32-kori változata (lapforrás) SweidanO (vitalap | szerkesztései) (→‎Megoldás) ← Régebbi szerkesztés		A lap 2015. november 3., 14:25-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) a (→‎Megoldás) Újabb szerkesztés →
16. sor:		16. sor:
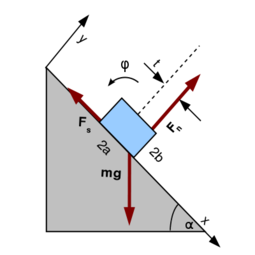
	<wlatex>A mozgásegyenletek az ábra koordinátarendszerében: $$m\ddot x=mg\sin{\alpha}-F_s$$ $$m\ddot y=F_{ny}-mg\cos{\alpha}$$ $$\theta\ddot\varphi=F_{ny}t-F_sb$$ Mivel a test csúszik, biztosan nem billen fel, tehát $\ddot y=0$ és $\ddot\varphi=0$, így $F_{ny}=mg\cos{\alpha}$, $F_s=\mu mg\cos{\alpha}$, így $t=\mu b=0,01\,m$. Tovább növelve $\mu$ értékét $t$ is növekszik, de $t>a$ nem lehetséges. Amíg $\mu\leq\frac ab=2$, addig biztosan nem billen, mert csúszik.		<wlatex>A mozgásegyenletek az ábra koordinátarendszerében: $$m\ddot x=mg\sin{\alpha}-F_s$$ $$m\ddot y=F_{ny}-mg\cos{\alpha}$$ $$\theta\ddot\varphi=F_{ny}t-F_sb$$ Mivel a test csúszik, biztosan nem billen fel, tehát $\ddot y=0$ és $\ddot\varphi=0$, így $F_{ny}=mg\cos{\alpha}$, $F_s=\mu mg\cos{\alpha}$, így $t=\mu b=0,01\,m$. Tovább növelve $\mu$ értékét $t$ is növekszik, de $t>a$ nem lehetséges. Amíg $\mu\leq\frac ab=2$, addig biztosan nem billen, mert csúszik.
	Ha $\mu>\frac ab=2$, nem csúszik, hanem tapad, így $\ddot x=0$ Tegyük fel, hogy továbbra sem billen, így a többi mozgásegyenletből $t=b\tan{\alpha}$, ami továbbra sem lehet nagyobb, mint $a$, tehát $\tan{\alpha}<=\frac ab=2$. Jelen téglatest esetében a lejtő nem elég meredek a billenéshez még nagyon nagy súrlódási együttható mellett sem.		Ha $\mu>\frac ab=2$, nem csúszik, hanem tapad, így $\ddot x=0$ Tegyük fel, hogy továbbra sem billen, így a többi mozgásegyenletből $t=b\tan{\alpha}$, ami továbbra sem lehet nagyobb, mint $a$, tehát $\tan{\alpha}<=\frac ab=2$. Jelen téglatest esetében a lejtő nem elég meredek a billenéshez még nagyon nagy súrlódási együttható mellett sem.
−	Érdemes kvalitatíve is megvizsgálni, hogy összességében mik a billenés feltételei. Egyrészt azt látjuk, hogy a lejtőnek elég meredeknek kell lennie, hogy a súlyerő hatásvonala a test alsó éléhez képest a lejtő alja felé legyen. Másrészt a test nem csúszhat meg a kellően meredek, vagy annál kisebb szögű lejtőn. További esetek: ha a lejtő nem elég meredek, akkor a súrlódási tényezőtől függően csúszás vagy tapadás lesz. Ha a lejtő elég meredek, viszont a súrlódási együttható nem elég nagy, akkor csúszik a test.[[Kép:Kfgy_3_3_29M.svg |none|250px]]</wlatex>	+	Érdemes kvalitatíve is megvizsgálni, hogy összességében mik a billenés feltételei. Egyrészt azt látjuk, hogy a lejtőnek elég meredeknek kell lennie, hogy a súlyerő hatásvonala a test alsó éléhez képest a lejtő alja felé legyen. Másrészt a test nem csúszhat meg a kellően meredek, vagy annál kisebb szögű lejtőn. További esetek: ha a lejtő nem elég meredek, akkor a súrlódási tényezőtől függően csúszás vagy tapadás lesz. Ha a lejtő elég meredek, viszont a súrlódási együttható nem elég nagy, akkor csúszik a test.[[Kép:Kfgy_3_3_29M.svg |none|255px]]</wlatex>
	</noinclude>		</noinclude>

---

A lap 2015. november 3., 14:25-kori változata

[rejt] Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Merev testek II.
Feladatok listája: Korongon mozgatott tömegpont Lelógatott korong Lelógatott korong tárcsával és tömeggel Lépcsős csiga Tömeg rugón súlyos csigával Korong vízszintes talajon húzva Henger lejtőn Három test lejtőn Forgó henger lejtőn húzva Hokikorong és rúd ütközése Hokikorong és rúd ütközése II Felbillenés lejtőn
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

1. (*3.3.29.) Egy 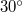hajlásszögű lejtőn 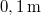magasságú, 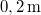hosszú és 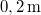szélességű test csúszik le. A test tömege 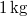. A test és a lejtő felülete között a súrlódási tényező .

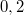   a) Írja fel a test mozgásegyenletét!

   b) Hol van a test és a lejtő kölcsönhatását számbavevő erők támadáspontja?

   c) Létezhet-e akkora súrlódási tényező, hogy a test felbillenjen?

Megoldás

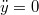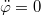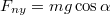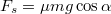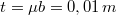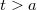A mozgásegyenletek az ábra koordinátarendszerében: Mivel a test csúszik, biztosan nem billen fel, tehát és , így , , így . Tovább növelve értékét is növekszik, de nem lehetséges. Amíg 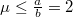, addig biztosan nem billen, mert csúszik.

Ha 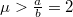, nem csúszik, hanem tapad, így 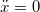Tegyük fel, hogy továbbra sem billen, így a többi mozgásegyenletből 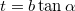, ami továbbra sem lehet nagyobb, mint , tehát 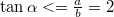. Jelen téglatest esetében a lejtő nem elég meredek a billenéshez még nagyon nagy súrlódási együttható mellett sem.

Érdemes kvalitatíve is megvizsgálni, hogy összességében mik a billenés feltételei. Egyrészt azt látjuk, hogy a lejtőnek elég meredeknek kell lennie, hogy a súlyerő hatásvonala a test alsó éléhez képest a lejtő alja felé legyen. Másrészt a test nem csúszhat meg a kellően meredek, vagy annál kisebb szögű lejtőn. További esetek: ha a lejtő nem elég meredek, akkor a súrlódási tényezőtől függően csúszás vagy tapadás lesz. Ha a lejtő elég meredek, viszont a súrlódási együttható nem elég nagy, akkor csúszik a test.