„Elektrosztatika példák - Különböző vezetőképességű anyagok határfelületén az átfolyó áram hatására kialakuló felületi töltéssűrűség.” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Feladat) |
||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
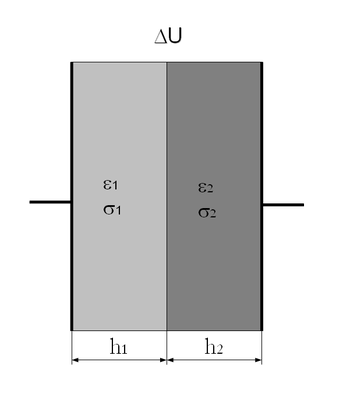
| − | </noinclude><wlatex>#Egy síkkondenzátor fegyverzetek közötti terét két vezető lemezzel töltjük ki. A lemezek egymással és a kondenzátor lemezeivel teljes felületükön érintkeznek. A lemezek vastagsága $h_1$ és $h_2$, vezetőképességük és dielektromos állandójuk $\sigma_1$,$\sigma_2$, illetve $\epsilon_1$ $\epsilon_2$. A kondenzátorlemezek (melyek $\sigma_1$-nél és $\sigma_2$-nél jóval nagyobb vezetőképességű anyagból készültek) között adott a potenciálkülönbség: $\Delta U$. Határozzuk meg az elektromos tér, valamint az elektromos eltolás nagyságát! Határozzuk meg az áramsűrűség nagyságát a közegekben, továbbá a stacionárius áramok hatására kialakuló felületi töltéssűrűséget![[Kép:KFGY2-5-4.png|none|350px]]</wlatex><includeonly><wlatex>{{Végeredmény|content=$$D_2 A-D_1 A =\omega A \rightarrow \omega = D_2-D_1 = \frac{\Delta U\epsilon_0\cdot \left(\epsilon_2\sigma_1-\epsilon_1\sigma_2\right)}{\sigma_2 h_1+\sigma_1 h_2} $$. | + | </noinclude><wlatex>#Egy síkkondenzátor fegyverzetek közötti terét két vezető lemezzel töltjük ki. A lemezek egymással és a kondenzátor lemezeivel teljes felületükön érintkeznek. A lemezek vastagsága $h_1$ és $h_2$, vezetőképességük és dielektromos állandójuk $\sigma_1$,$\sigma_2$, illetve $\epsilon_1$ $\epsilon_2$. A kondenzátorlemezek (melyek $\sigma_1$-nél és $\sigma_2$-nél jóval nagyobb vezetőképességű anyagból készültek) között adott a potenciálkülönbség: $\Delta U$. Határozzuk meg az elektromos tér, valamint az elektromos eltolás nagyságát! Határozzuk meg az áramsűrűség nagyságát a közegekben, továbbá a stacionárius áramok hatására kialakuló felületi töltéssűrűséget! A síkkondenzátot ideálisnak tételezzük fel, azaz a szélein kialakuló szórt tértől tekintsünk el![[Kép:KFGY2-5-4.png|none|350px]]</wlatex><includeonly><wlatex>{{Végeredmény|content=$$D_2 A-D_1 A =\omega A \rightarrow \omega = D_2-D_1 = \frac{\Delta U\epsilon_0\cdot \left(\epsilon_2\sigma_1-\epsilon_1\sigma_2\right)}{\sigma_2 h_1+\sigma_1 h_2} $$.}} |
</wlatex></includeonly><noinclude> | </wlatex></includeonly><noinclude> | ||
A lap 2021. március 22., 13:31-kori változata
Feladat
- Egy síkkondenzátor fegyverzetek közötti terét két vezető lemezzel töltjük ki. A lemezek egymással és a kondenzátor lemezeivel teljes felületükön érintkeznek. A lemezek vastagsága
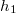és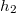 
, vezetőképességük és dielektromos állandójuk 
,
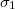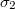, illetve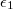 
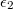. A kondenzátorlemezek (melyek 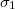-nél és 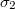-nél jóval nagyobb vezetőképességű anyagból készültek) között adott a potenciálkülönbség: 
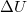. Határozzuk meg az elektromos tér, valamint az elektromos eltolás nagyságát! Határozzuk meg az áramsűrűség nagyságát a közegekben, továbbá a stacionárius áramok hatására kialakuló felületi töltéssűrűséget! A síkkondenzátot ideálisnak tételezzük fel, azaz a szélein kialakuló szórt tértől tekintsünk el!
Megoldás
A kontinuitási tétel miatt:
![\[j_1 = j_2 = j\]](/images/math/9/9/b/99bcf214f7711c8a889515db78711714.png)
Mindkét közegben érvényes a differenciális Ohm-törvény:
![\[E_1 = \frac{j}{\sigma_1}\]](/images/math/3/d/2/3d2cd921d089f5fcf3930390011d0b92.png)
![\[E_2 = \frac{j}{\sigma_2}\]](/images/math/7/4/3/7435c382efe8e8a739a0d8a606b7e411.png)
A lemezek közötti potenciálkülönbség pedig:
![\[\Delta U = E_1 h_1 +E_2 h_2 = j \Big( \frac{h_1}{\sigma_1} + \frac{h_2}{\sigma_2} \Big)\]](/images/math/6/0/2/6027870d084426f7bd4deed3aa86c0c9.png)
Ebből kifejezve az áramsűrűséget kapjuk, hogy
![\[j = \frac{\Delta U \sigma_1 \sigma_2}{\sigma_2 h_1+\sigma_1 h_2}\]](/images/math/0/8/5/0854b17e037b4861fdb577fc399592cd.png)
Innen a térerősségek:
![\[E_1 = \frac{\Delta U \sigma_2}{\sigma_2 h_1+\sigma_1 h_2}\]](/images/math/7/5/3/7536faeeaba9eb92e1a1006e90b11957.png)
![\[E_2 = \frac{\Delta U \sigma_1}{\sigma_2 h_1+\sigma_1 h_2}\]](/images/math/7/b/3/7b3b95f8efeb9be3685088919847a819.png)
Az elektromos eltolások pedig a két közegben:
![\[D_1 = \epsilon_0 \epsilon_1 E_1 = \frac{\Delta U \sigma_2 \epsilon_0\epsilon_1}{\sigma_2 h_1+\sigma_1 h_2}\]](/images/math/4/f/1/4f1e5a6b72067faeaa5c3ee218ae4c15.png)
![\[D_2 = \epsilon_0 \epsilon_2 E_2 = \frac{\Delta U \sigma_1 \epsilon_0\epsilon_2}{\sigma_2 h_1+\sigma_1 h_2}\]](/images/math/a/3/b/a3b7207b677c5b33e439cb8413690074.png)
A határfelületen felhalmozódott töltést pedig a Gauss-tételből lehet kiszámolni
![\[ \iint \vec{D} \vec{dA} = Q\]](/images/math/2/f/0/2f0569c3673a40eac616da205f160f16.png)
ahol a Gauss felület egy olyan téglatest, amely a határfelületet zárja be és csak a határfelülettel párhuzamos és rá merőleges oldallapjai vannak.
![\[D_2 A-D_1 A =\omega A \rightarrow \omega = D_2-D_1 = \frac{\Delta U \epsilon_0\cdot \left(\epsilon_2\sigma_1-\epsilon_1\sigma_2\right)}{\sigma_2 h_1+\sigma_1 h_2} \]](/images/math/d/9/2/d9243be3972e5031ee5f1932c3081ebe.png)
