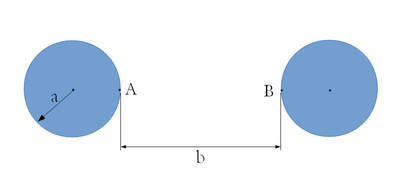
Elektrosztatika példák - Párhuzamos hengeres vezetékek kapacitása
Feladat
- Két azonos,
 keresztmetszeti sugarú,
keresztmetszeti sugarú,  hosszúságú hengeres vezeték fekszik egymás mellett párhuzamosan, egymástól
hosszúságú hengeres vezeték fekszik egymás mellett párhuzamosan, egymástól 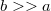 távolságra. Mekkora a rendszer kapacitása? (
távolságra. Mekkora a rendszer kapacitása? (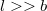 )
)
Megoldás
Legyen  felületi töltéssűrűség az egyik,
felületi töltéssűrűség az egyik,  felületi töltéssűrűség a másik hengeren.
felületi töltéssűrűség a másik hengeren.
Először próbáljuk meghatározni kizárólag az  töltéssűrűségű hengerfelület által keltett elektromos teret. Ehhez vegyünk fel egy
töltéssűrűségű hengerfelület által keltett elektromos teret. Ehhez vegyünk fel egy 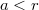 sugarú,
sugarú,  hosszúságú hengerfelületet, melynek tengelye egybe esik a fémhenger tengelyével. A hengerfelület által bezárt töltés mennyisége könnyen kiszámítható, hiszen az
hosszúságú hengerfelületet, melynek tengelye egybe esik a fémhenger tengelyével. A hengerfelület által bezárt töltés mennyisége könnyen kiszámítható, hiszen az  sugarú fémhenger
sugarú fémhenger  hosszúságú darabját zárja be. Tehát a bezárt töltés:
hosszúságú darabját zárja be. Tehát a bezárt töltés:
![\[Q=2\pi a l \omega\]](/images/math/d/d/3/dd37de0c573673601f0220a7b1e57e87.png)
A bezárt  töltés ismeretében felírhatjuk az
töltés ismeretében felírhatjuk az  sugarú hengerfelületre a Gauss-törvényt:
sugarú hengerfelületre a Gauss-törvényt:
![\[\dfrac{Q}{\varepsilon_0}=\dfrac{2\pi a l \omega}{\varepsilon_0}=\oint\overline{EdA}\]](/images/math/c/c/d/ccd982eff34727d3bf8db593b87cf73e.png)
Az elrendezés hengerszimmetriája miatt az elektromos térerősség vektora mindenütt merőleges az  sugarú hengerpalást felületére, és nagysága is mindenütt megegyező, ezért az integrál a következőképp egyszerűsödik:
sugarú hengerpalást felületére, és nagysága is mindenütt megegyező, ezért az integrál a következőképp egyszerűsödik:
![\[\dfrac{2\pi a l \omega}{\varepsilon_0}=\oint\overline{EdA}=2\pi r l E\]](/images/math/1/b/e/1be3bdc728c122db1bf4a9399864f2bd.png)
Kifejezve  -t, megkapjuk a térerősséget a kondenzátor tengelyétől mért távolság függvényében:
-t, megkapjuk a térerősséget a kondenzátor tengelyétől mért távolság függvényében:
![\[E_{(r)}=\dfrac{\omega a}{\varepsilon_0}\dfrac{1}{r}\]](/images/math/c/4/1/c41f0c8ce47d424c168f96d1da538f58.png)
Az  felületi töltéssűrűséggel rendelkező henger által keltett tér hatására
felületi töltéssűrűséggel rendelkező henger által keltett tér hatására 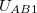 potenciálkülönbség jön létre az 1. ábrán látható A és B pontok között. Az
potenciálkülönbség jön létre az 1. ábrán látható A és B pontok között. Az 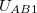 meghatározható, ha az
meghatározható, ha az  felületi töltéssűrűséggel rendelkező henger elektromos terét integráljuk
felületi töltéssűrűséggel rendelkező henger elektromos terét integráljuk  és
és  pontok között:
pontok között:
![\[U_{AB1}=-\int_{A}^{B}E_{(r)}dr-\int_{a}^{b-a}E_{(r)}dr=-\dfrac{\omega a}{\varepsilon_0} \int_{a}^{b-a} \dfrac{1}{r} dr=\dfrac{\omega a}{\varepsilon_0} ln \left( \dfrac{b-a}{a} \right)\]](/images/math/8/f/b/8fb996a3bdecf42394b68fdf5533650d.png)
A két hengerből álló rendszer tükörszimmetriájából következik, hogy a másik,  töltéssűrűségű henger által az
töltéssűrűségű henger által az  és
és  pontok között létrehozott
pontok között létrehozott 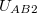 potenciálkülönbség megegyezik az első henger által keltett
potenciálkülönbség megegyezik az első henger által keltett 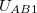 potenciálkülönbséggel. (
potenciálkülönbséggel. (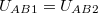 ) Tekintve, hogy a potenciáltér lineáris, a két hengerfelület között mért potenciálkülönbség az egyes hengerek által keltett potenciálkülönbségek összege:
) Tekintve, hogy a potenciáltér lineáris, a két hengerfelület között mért potenciálkülönbség az egyes hengerek által keltett potenciálkülönbségek összege:
![\[U_{AB}=U_{AB1}+U_{AB2}=2U_{AB1}=\dfrac{2\omega a}{\varepsilon_0} ln \left( \dfrac{b-a}{a} \right)\]](/images/math/7/0/d/70dafe8fe0d2954c45878f5dd6bfc4e7.png)
A rendszer kapacitása:
![\[C=\dfrac{Q}{U_{AB}}=\dfrac{Q=2\pi a l \omega}{\dfrac{2\omega a}{\varepsilon_0} ln \left( \dfrac{b-a}{a} \right)}=\dfrac{\pi l \varepsilon_0}{ln \left( \dfrac{b-a}{a} \right)}\]](/images/math/0/c/3/0c32ac863e4b3b202ac8f4a34725cbf6.png)