Mechanika - Lelógatott korong tárcsával és tömeggel
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. december 29., 18:43-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*3.3.7.)
 sugarú
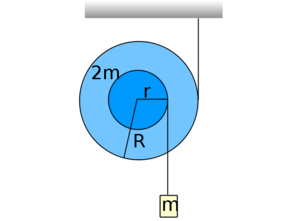
sugarú 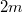 tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű
tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű  sugarú tárcsa kerületére csavart fonál végére
sugarú tárcsa kerületére csavart fonál végére  tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását!
tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását!
Megoldás
Legyen a korong az 1-es test, az azt tartó kötélerő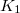 , a másik test a 2-es, és a kettő közti kötélben ható erő
, a másik test a 2-es, és a kettő közti kötélben ható erő 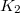 . A megadott adatokkal
. A megadott adatokkal 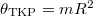 . A mozgásegyenletek mozgásirányban pozitív koordinátatengelyekkel
. A mozgásegyenletek mozgásirányban pozitív koordinátatengelyekkel ![\[ma_2=mg-K_2\]](/images/math/4/4/f/44fd22fda75c437123f446440acbe621.png)
![\[2ma_1=2mg+K_2-K_1\]](/images/math/3/5/f/35f9ecc4fc15ab0cef5014726ced033d.png)
![\[\theta_{\rm{TKP}}\beta=mR^2\cdot\beta=K_1R-K_2r\]](/images/math/4/d/7/4d78d25406c78ab8df740d9c2b92244b.png)
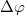 szögben elfordul. Mivel ekkor
szögben elfordul. Mivel ekkor 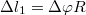 hosszúságú kötél csavarodik le a korongról, kétszeres időderiválással
hosszúságú kötél csavarodik le a korongról, kétszeres időderiválással 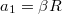 . Emiatt a másik test
. Emiatt a másik test 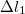 -el lejjebb kerülne, de közben a tárcsán felcsavarodik
-el lejjebb kerülne, de közben a tárcsán felcsavarodik 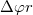 hosszúságú kötél, emiatt ennyivel feljebb kerülne. Összességében tehát
hosszúságú kötél, emiatt ennyivel feljebb kerülne. Összességében tehát 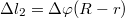 a magasságváltozás, ezt kétszer idő szerint deriválva
a magasságváltozás, ezt kétszer idő szerint deriválva 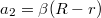 . Áttérve a szöggyorsulásra és
. Áttérve a szöggyorsulásra és 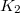 -t behelyettesítve az első mozgásegyenletből a másik kettőbe már csak két ismeretlen és két egyenlet van. A második mozgásegyenletet
-t behelyettesítve az első mozgásegyenletből a másik kettőbe már csak két ismeretlen és két egyenlet van. A második mozgásegyenletet  -el szorozva a másik kötélerőtől is meg lehet válni az egyenletek összeadásával, így kapható a szöggyorsulásra
-el szorozva a másik kötélerőtől is meg lehet válni az egyenletek összeadásával, így kapható a szöggyorsulásra ![\[\beta=g\frac{6R-2r}{8R^2+2r^2-4rR}\]](/images/math/4/c/b/4cb2890bf3e7604cd4b163ff532dedb8.png)