Elektrosztatika példák - Hengerfelületre feltekert síkkondenzátor
Feladat
- Adott egy síkkondenzátor, melynek fegyverzetei egymástól \textit{d} távolságra helyezkednek el. A kondenzátort feltekerjük egy vastag, \textit{r} sugarú hengerre úgy, hogy annak palástján a fegyverzetek \textit{N} réteget alkotnak az 1. ábra szerint. Mennyivel változik az így kapott kondenzátor kapacitása az eredeti állapotához képest? Tételezzük fel, hogy a feltekert fegyverzetek sok réteget alkotnak (
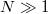 ), és a rétegrendszer teljes vastagsága lényegesen kisebb, mint a henger sugara (
), és a rétegrendszer teljes vastagsága lényegesen kisebb, mint a henger sugara (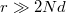 ).
).
Megoldás
Ha 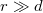 , akkor a fóliák közti térerősség rendre {
, akkor a fóliák közti térerősség rendre {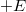 ,
, 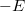 ,
, 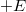 ,
, 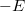 ...} (2. ábra) ahol
...} (2. ábra) ahol 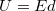 a fóliák között mérhető potenciálkülönbség.
a fóliák között mérhető potenciálkülönbség.
2. ábra
Hogy megállapítsuk a legbelső, pozitív töltésű fóliarétegen található 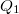 töltés mennyiségét, felvesszük a 3. ábra szerinti felületet, és alkalmazzuk rá a Gauss törvényt.
töltés mennyiségét, felvesszük a 3. ábra szerinti felületet, és alkalmazzuk rá a Gauss törvényt.
3. ábra
Belátható, hogy:
-A felvett felület csak a belső, 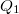 töltésű fóliaréteget zárja magába.
-A felvett felület területű palástján mindenütt normális irányú, kifelé mutató
töltésű fóliaréteget zárja magába.
-A felvett felület területű palástján mindenütt normális irányú, kifelé mutató  térerősség mérhető.
-A többi záró felületen a térerősségnek nincs felületre merőleges komponense.
Ezek alapján a Gauss törvény:
térerősség mérhető.
-A többi záró felületen a térerősségnek nincs felületre merőleges komponense.
Ezek alapján a Gauss törvény:
![\[ 2\pi rlE=\dfrac{Q_{1}}{\varepsilon_{0}} \]](/images/math/5/2/5/525f05289a6c2d6d92b047175c0f1fb8.png)
Az első fóliaréteg töltése tehát:
![\[ Q_{1}=2\pi rl\varepsilon_{0}E \]](/images/math/6/c/d/6cd839b46da5522d2ec8c3a23445d693.png)
A második, negatív töltésű fóliarétegen található {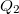 } töltést az 4. ábra szerinti Gauss-felület felvételével határozzuk meg.
} töltést az 4. ábra szerinti Gauss-felület felvételével határozzuk meg.
4. ábra
Megállapítható, hogy:
-Az új felület a már ismert 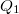 és a még ismeretlen
és a még ismeretlen 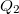 töltést zárja magába.
-A paláston mindenütt normális irányú, befelé mutató
töltést zárja magába.
-A paláston mindenütt normális irányú, befelé mutató  térerősség mérhető.
-A többi záró felületen a térerősségnek nincs felületre merőleges komponense.
Ezek alapján a Gauss törvény:
térerősség mérhető.
-A többi záró felületen a térerősségnek nincs felületre merőleges komponense.
Ezek alapján a Gauss törvény:
![\[ 2\pi rl(-E)=\dfrac{Q_{1}+Q_{2}}{\varepsilon_{0}} \]](/images/math/0/5/6/056a9e1d438e2503a684a7e5e472f6d2.png)
A második fóliaréteg töltése tehát:
![\[ Q_{2}=-2Q_{1} \]](/images/math/4/e/9/4e95be60bfe7a7b8797e8a6cb2607050.png)
A harmadik fóliaréteg is magába záró felületre felírt Gauss törvény a fentiek alapján:
![\[ 2\pi rlE=\dfrac{Q_{1}+Q_{2}+Q_{3}}{\varepsilon_{0}} \]](/images/math/5/b/8/5b8d809aab98be6241ad82dc931ed3d7.png)
A harmadik fóliaréteg töltése:
![\[ Q_{3}=2Q_{1} \]](/images/math/6/8/4/684ad69fa0e18aa17032b753c65a27a7.png)
Ha a Gauss tételt sorban alkalmazzuk olyan zárt felületekre, amelyek rendre egyel több fóliaréteget zárnak magukba az előzőleg felvett felülethez képest, beláthatjuk, hogy a töltés az egyes fóliarétegeken az 5. ábra szerint alakul.
5. ábra
A legkülső felületen szükségszerűen 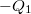 töltésnek kell lenni, hogy a rendszer kifelé semlegesnek mutatkozzék.
töltésnek kell lenni, hogy a rendszer kifelé semlegesnek mutatkozzék.
Egy fegyverzeten található össztöltés  db tekeredés esetén:
db tekeredés esetén:
![\[ Q=Q_{1}+2Q_{1}+2Q_{1}+...+2Q_{1}=(2N-1)\dfrac{A}{N}\varepsilon_{0}E \]](/images/math/7/8/0/78096c3eca945ac65913a70f0884bfe0.png)
Ahol 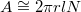 a fólia területe.
a fólia területe.
A lemezek közti feszültség 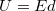 , tehát a kapacitás:
, tehát a kapacitás:
![\[C=\dfrac{Q}{U}=\dfrac{\dfrac{2N-1}{N}A\varepsilon_{0}E}{Ed}=\dfrac{2N-1}{N}\varepsilon_{0}\dfrac{A}{d} \]](/images/math/b/4/0/b407bccfa069329440f1af6e284f3724.png)
A síkkondenzátor 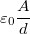 kapacitása
kapacitása 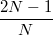 -szeresére nőtt a feltekerés hatására.
Ha
-szeresére nőtt a feltekerés hatására.
Ha  igen nagy,
igen nagy, 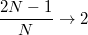 , tehát a kapacitás kétszeresére nő.
, tehát a kapacitás kétszeresére nő.