Mechanika - Korongon mozgatott tömegpont

Feladat

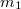1. *3.3.5. $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű, $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, függőleges tengely körül súrlódás nélkül forgó korong kerületén $\setbox0\hbox{$m_1$}% \message{//depth:\the\dp0//}% \box0%$ tömegű pontszerű test van rögzítve. A rendszer $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ szögsebességgel forog. 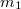Mekkora munka árán lehet az $\setbox0\hbox{$m_1$}% \message{//depth:\the\dp0//}% \box0%$ tömegpontot a forgástengelyhez hozni? (A tömegpontot pl. súrlódásmentes csatornában húzzuk a centrum felé.)

Megoldás

Mivel a tömegpontot sugárirányú erővel húzzuk a tengelyhez, arra vonatkoztatva nincs forgatónyomatéka, viszont munkavégzése van, így a rendszer összes perdülete nem, csak a mozgási energiája változik meg, ami épp a keresett munkavégzés. A kezdeti és a végállapotbeli együttes tehetetlenségi nyomatékot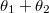 $\setbox0\hbox{$\theta_1+\theta_2$}% \message{//depth:\the\dp0//}% \box0%$-vel és 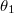$\setbox0\hbox{$\theta_1$}% \message{//depth:\the\dp0//}% \box0%$-el jelölve a munkavégzés

$\[W=\frac12\omega^2\frac{\theta_2^2+\theta_1 \theta_2}{\theta_1}=\frac12\omega^2m_1R^2\left(\frac{2m_1}m+1\right)\]$