Mechanika - Merev testek II.
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. november 12., 17:36-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- (*3.3.5.)
 tömegű,
tömegű,  sugarú, függőleges tengely körül súrlódás nélkül forgó korong kerületén
sugarú, függőleges tengely körül súrlódás nélkül forgó korong kerületén 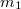 tömegű pontszerű test van rögzítve. A rendszer
tömegű pontszerű test van rögzítve. A rendszer  szögsebességgel forog. Mekkora munka árán lehet az
szögsebességgel forog. Mekkora munka árán lehet az 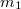 tömegpontot a forgástengelyhez hozni? (A tömegpontot pl. súrlódásmentes csatornában húzzuk a centrum felé.)
tömegpontot a forgástengelyhez hozni? (A tömegpontot pl. súrlódásmentes csatornában húzzuk a centrum felé.)
- (3.3.6.)
 sugarú
sugarú  tömegű korong kerületére csavart fonál végét rögzítjük, és a korongot elengedjük.
tömegű korong kerületére csavart fonál végét rögzítjük, és a korongot elengedjük.
- a) Írjuk le a korong mozgását!
- b) Mekkora a korong
 szögsebessége és középpontjának
szögsebessége és középpontjának  sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról
sebessége, ha a korong kezdősebesség nélkül indult és mozgása során a korongról  hosszúságú fonaldarab csavarodott le?
hosszúságú fonaldarab csavarodott le?
- (*3.3.7.)
 sugarú
sugarú 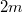 tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű
tömegű korong kerületére csavart fonál szabad végét felfüggesztjük. A koronghoz erősített elhanyagolható tömegű  sugarú tárcsa kerületére csavart fonál végére
sugarú tárcsa kerületére csavart fonál végére  tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását!
tömegű testet függesztünk (mindkét fonál a korong középpontjának ugyanazon oldalán van). A rendszer függőleges síkban mozoghat. Írjuk le a rendszer mozgását!
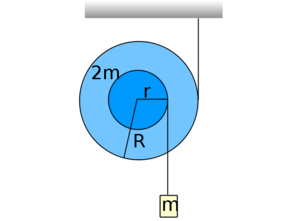
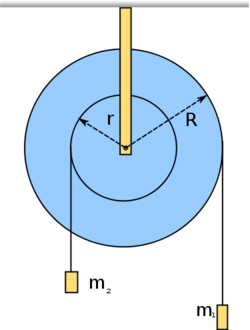
- (*3.3.8.) Az ábrán feltüntetett
 tehetetlenségi nyomatékú lépcsős csiga két kötelére
tehetetlenségi nyomatékú lépcsős csiga két kötelére 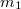 és
és 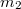 tömegű súlyokat függesztünk. Határozzuk meg a csiga szöggyorsulását, és a kötélágakban ébredő erőket!
tömegű súlyokat függesztünk. Határozzuk meg a csiga szöggyorsulását, és a kötélágakban ébredő erőket!
Mechanika - abc
Mechanika - abc
Mechanika - abc
Mechanika - abc
Mechanika - abc
Mechanika - abc
![\[W=\frac12\omega^2m_1R^2\left(\frac{2m_1}m+1\right)\]](/images/math/c/2/8/c28609ebe704254142dd1a0500b2ae41.png)

![\[\beta=\frac{2g}{3R}\]](/images/math/c/6/a/c6af796891b7a163698d29903524966c.png)
![\[K=\frac{mg}3\]](/images/math/5/2/7/52725fae775e2fae11b0ff221c1c53ea.png)
![\[\omega=\sqrt{\frac{4gl}{3R^2}}\]](/images/math/5/9/d/59d2cc5504905104ac1e8e187ab1e258.png)
![\[v=\sqrt{\frac43 gl}\]](/images/math/5/7/a/57a92411e8d0a4b01ec5b3e9920a3958.png)
![\[\beta=g\frac{6R-2r}{8R^2+2r^2-4rR}\]](/images/math/4/c/b/4cb2890bf3e7604cd4b163ff532dedb8.png)
![\[\beta=\frac{m_1gR-m_2gr}{m_1R^2+m_2r^2+\theta}\]](/images/math/a/6/b/a6b10a5a3ca6e0c94124a48c3fde35ee.png)