Elektrosztatika példák - Hengerkondenzátor kapacitása

Feladat

1. Számítsuk ki egy $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú, 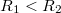$\setbox0\hbox{$R_1<R_2$}% \message{//depth:\the\dp0//}% \box0%$ sugarakkal rendelkező hengerkondenzátor kapacitását, ha a hengerek között levegő van.

Megoldás

Legyen $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ felületi töltéssűrűség a belső, $\setbox0\hbox{$R_1$}% \message{//depth:\the\dp0//}% \box0%$ sugarú hengeren. Próbáljuk meghatározni a két hengerfelület közti elektromos teret. Ehhez vegyünk fel egy 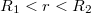$\setbox0\hbox{$R_1<r<R_2$}% \message{//depth:\the\dp0//}% \box0%$ sugarú, $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú hengerfelületet, melynek tengelye egybe esik a kondenzátor tengelyével. A henger által bezárt töltés mennyisége könnyen kiszámítható, hiszen az a kondenzátor belső, $\setbox0\hbox{$R_1$}% \message{//depth:\the\dp0//}% \box0%$ sugarú fegyverzetének $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú darabját zárja be. Tehát a bezárt töltés:

$\[Q=2\pi R_1 l \omega\]$

A bezárt $\setbox0\hbox{$Q$}% \message{//depth:\the\dp0//}% \box0%$ töltés ismeretében felírhatjuk az $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ sugarú hengerfelületre a Gauss-törvényt:

$\[\dfrac{Q}{\varepsilon_0}=\dfrac{2\pi R_1 l \omega}{\varepsilon_0}=\oint\overline{EdA}\]$

A rendszer hengerszimmetriája miatt az elektromos térerősség vektora mindenütt merőleges az $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ sugarú hengerpalást felületére, és nagysága is mindenütt megegyező, ezért az integrál a következőképp egyszerűsödik:

$\[\dfrac{2\pi R_1 l \omega}{\varepsilon_0}=\oint\overline{EdA}=2\pi r l E\]$

Kifejezve $\setbox0\hbox{$E$}% \message{//depth:\the\dp0//}% \box0%$-t, megkapjuk a térerősséget a kondenzátor tengelyétől mért távolság függvényében:

$\[E_{(r)}=\dfrac{\omega R_1}{\varepsilon_0}\dfrac{1}{r}\]$

A térerősség ismeretében meghatározhatjuk a két hengerfelület közti potenciálkülönbséget:

$\[U_{1,2}=-\int_{R_1}^{R_2}E_{(r)}dr=-\dfrac{\omega R_1}{\varepsilon_0} \int_{R_1}^{R_2} \dfrac{1}{r} dr=\dfrac{\omega R_1}{\varepsilon_0} ln \left( \dfrac{R_2}{R_1} \right)\]$

A kapacitás pedig:

$\[C=\dfrac{Q}{U_{1,2}}=\dfrac{2\pi R_1 l \omega}{\dfrac{\omega R_1}{\varepsilon_0} ln \left( \dfrac{R_2}{R_1} \right)}=\dfrac{2\pi l \varepsilon_0}{ln \left( \dfrac{R_2}{R_1} \right)}\]$

$\[C=\dfrac{Q}{U}=4\pi\varepsilon_0 R\]$