Elektrosztatika példák - Síkkondenzátoron végzett munka
Feladat
- Síkkondenzátor
területű lemezei között levegő van. Mennyi munkát kell végezni ahhoz, hogy a lemezek közötti távolságot lassan 
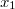-ről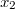 
-re növeljük, ha a folyamat során
a) a lemezekre vitt
töltést;
b) a lemezek közötti
feszültséget tartjuk állandónak?
Megoldás
a)
Ha a lemezeken levő töltés álladó, akkor gyakorlatilag a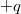 
töltésű lemez terében mozgatjuk a 
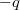töltésű másik lemezt. A mozgatáshoz szükséges munkavégzést kell kiszámítani. A 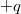töltésű lemez felületi töltéssűrűsége:
![\[\omega=\dfrac{q}{S}\]](/images/math/9/4/a/94a6867239d8dd3dbafec6a0fdfca842.png)
A nagy kiterjedésű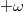 
töltésű lemez által keltett elektromos tér nagysága Gauss törvény segítségével könnyen kiszámítható (1. feladatsor 9. feladat)
![\[E=\dfrac{\omega}{2\varepsilon_0}=\dfrac{q}{2S\varepsilon_0}\]](/images/math/c/c/b/ccbafe1b14100179565bb522b3c285ba.png)
Ebben az elektromos térben a 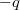töltésű lemezre ható erő:
![\[F=-qE=-\dfrac{q^2}{2S\varepsilon_0}\]](/images/math/7/2/6/726214d707a057e2b9b208e4cb1b2fcf.png)
Az 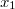-től 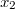-ig történő mozgatás során az erőtér munkája:
![\[W_{eroter}=F(x_2-x_1)=-\dfrac{q^2}{2S\varepsilon_0}(x_2-x_1)\]](/images/math/8/8/b/88b8324bff40222bd424c6cda7041f2e.png)
Mivel az erőtér által kifejtett erő ellenében dolgozunk, a mi munkánk pont az ellentettje az erőtér munkájának:
![\[W=-W_{eroter}=\dfrac{q^2}{2S\varepsilon_0}(x_2-x_1)\]](/images/math/d/8/a/d8af3f1478b61c97dea5be6ece8d3d1f.png)
b)
Ha a lemezek közti potenciálkülönbség állandó, a lemezek közti tér könnyen meghatározható:
![\[E=\dfrac{U}{x}\]](/images/math/4/a/6/4a6328d2f389f54ad85cf666e58cfd97.png)
Tudvalevő, hogy ez a tér az 
és a 
töltésű lap által keltett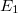 
és 
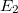térerősség-járulékokból tevődik össze. Kellően nagy felületek esetén a Gauss törvény segítségével meghatározható, hogy:
![\[|E_1|=|E_2|=\dfrac{\omega}{2\varepsilon_0}\]](/images/math/e/0/5/e05b65b6d05a77e7518d7a430b17c630.png)
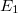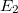Belátható továbbá az is, hogy a lemezek közti térben az és térerősség járulék egymást erősítve hozza létre az ott mérhető 
teret.
![\[E=|E_1|+|E_2|=\dfrac{\omega}{2\varepsilon_0}+\dfrac{\omega}{2\varepsilon_0}=\dfrac{\omega}{\varepsilon_0}\]](/images/math/c/a/1/ca1fa781b14312edb7389cad1e25f3f5.png)
A fentiek alapján felírhatjuk a a lemezek közti térerősségre az alábbi egyenletet:
![\[\dfrac{U}{x}=E=\dfrac{\omega}{\varepsilon_0}\]](/images/math/b/5/5/b55973f2fbff27d94b164c2ab58402da.png)
Melyből az ismeretlen felületi töltéssűrűséget kifejezve:
![\[\omega=\dfrac{\varepsilon_0 U}{x}\]](/images/math/1/1/4/114800fb9dc1ea0a6b8fc587da7215d4.png)
Ez alapján már meg tudjuk határozni, hogy a 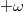töltéssűrűségű lemez 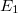elektromos terében mekkora erő hat a másik, 
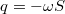töltésű lemezre az 
távolság függvényében:
![\[F=qE_1=-\omega S\dfrac{\omega}{2\varepsilon_0}=-\dfrac{\omega^2S}{2\varepsilon_0}=-\dfrac{\left(\dfrac{\varepsilon_0 U}{x} \right)^2S}{2\varepsilon_0}=-\dfrac{\varepsilon_0 U^2 S}{2 x^2}\]](/images/math/5/e/0/5e0c0178ab037e022b5fabaa84e8303a.png)
Az 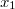-től 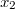-ig történő mozgatás során az erőtér munkája:
![\[W_{eroter}=\int_{x_1}^{x_2}F_{(x)}dx=-\dfrac{\varepsilon_0 U^2 S}{2}\int_{x_1}^{x_2} \dfrac{1}{x^2}dx=-\dfrac{\varepsilon_0 U^2 S}{2} \left( \dfrac{1}{x_1}-\dfrac{1}{x_2} \right)\]](/images/math/d/3/4/d342d29d5f3b1938132b685d5f6ce3ca.png)
Mivel az erőtér által kifejtett erő ellenében dolgozunk, a mi munkánk pont az ellentettje az erőtér munkájának:
![\[W=-W_{eroter}=\dfrac{\varepsilon_0 U^2 S}{2} \left( \dfrac{1}{x_1}-\dfrac{1}{x_2} \right)\]](/images/math/c/f/2/cf2cf313570b69799160c5967489a55c.png)
