Elektrosztatika példák - Dielektrikummal határolt végtelen töltött henger
Feladat
- Egy
 sugarú, végtelen hosszú fémhenger felületi töltéssűrűségre
sugarú, végtelen hosszú fémhenger felületi töltéssűrűségre  . A felületet egyenletes
. A felületet egyenletes  vastagságú,
vastagságú, 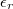 permittivitású réteggel vesszük körül.
permittivitású réteggel vesszük körül.
a) Mekkora a henger felületi töltéssűrűsége, ha egy töltést
töltést 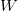 munka árán tudunk a henger tengelyétől
munka árán tudunk a henger tengelyétől 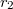 távolságból
távolságból 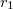 távolságba hozni.
távolságba hozni. ![\[r_2 > R_2+d > r_1 ??????\]](/images/math/6/4/c/64ca2ceaa38381d2c3a442fe9a21a6b8.png)
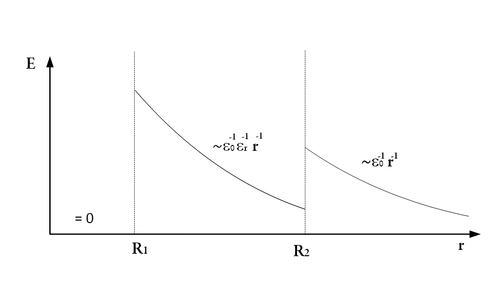
b) Ábrázoljuk, hogyan változik a térerősség a tengelytől mért távolság függvényében!
c) Mekkora maximális töltéssűrűség vihető a henger felületére, ha a dielektrikum átütési szilárdsága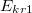 , a levegőé pedig
, a levegőé pedig 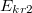 ?
?
Megoldás
a, Legyen a külső henger sugara 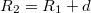 .
Írjuk fel a Gauss-tételt egy
.
Írjuk fel a Gauss-tételt egy  sugarú hengerfelületre, mely a töltött hengerrel koncentrikusan helyezkedik el. Így meghatározhatjuk az elektromos eltolás nagyságát:
sugarú hengerfelületre, mely a töltött hengerrel koncentrikusan helyezkedik el. Így meghatározhatjuk az elektromos eltolás nagyságát:
![\[D\cdot 2\cdot \pi\cdot L = \omega\cdot 2\cdot\pi\cdot R_1\cdot L\Rightarrow D = \frac{\omega\cdot R_1}{r}\]](/images/math/b/4/7/b47e1dda2b3506d99a75fbeaea1b8c9d.png)
Az elektromos térerősség a dielektrikumban:
![\[E = \frac{\omega\cdot R_1}{r\cdot\epsilon_0\cdot\epsilon_r}\]](/images/math/b/d/5/bd56ec4cf9c40499621e07ee9c2a6c9c.png)
A dielektrikumon kívül pedig:
![\[E = \frac{\omega\cdot R_1}{r\cdot\epsilon_0}\]](/images/math/4/2/9/429aa4ccccf5726ef718b2246b0e7d53.png)
A  töltésen végzett munka, miközben
töltésen végzett munka, miközben 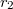 -ből
-ből 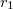 -be visszük:
-be visszük:
![\[W = q\cdot U_2-q\cdot U_1\]](/images/math/5/2/3/523a0172fabc2e3638fb7802f0410405.png)
Ha potenciál referencia pontját a hengertől egységnyi távolságra vesszük fel, akkor:
![\[U = \int_1^{R_2} \frac{\omega\cdot R_1}{r\cdot\epsilon_0}\cdot q dr+\int_{R_2}^{r_2} \frac{\omega\cdot R_1}{r\cdot\epsilon_0\cdot\epsilon_r}\cdot q dr-\int_1^{r_1} \frac{\omega\cdot R_1}{r\cdot\epsilon_0}\cdot q dr\]](/images/math/5/a/2/5a2ba4b8ccc698e0f0055057777b3fe2.png)
![\[U = \frac{\omega\cdot R_1\cdot q}{\epsilon_0}\ln\left(\left(\frac{r_2}{R_2}\right)^{\frac{1}{\epsilon_r}}\cdot\frac{R_2}{r_1}\right)\]](/images/math/a/d/3/ad327cedc7efb48e8deee3fd6be350ac.png)
Ebből kifejezhető a felületi töltéssűrűség:
![\[\omega = \frac{W\cdot \epsilon_0}{R_1\cdot q \cdot \ln\left(\left(\frac{r_2}{R_2}\right)^{\frac{1}{\epsilon_r}}\cdot\frac{R_2}{r_1}\right)}\]](/images/math/f/0/1/f01c11b27853a4a7434f56d0240dbf53.png)
b, A térerősséget ábrázolva
c, A dielektrikum akkor üt át, ha a benne lévő legnagyobb elektromos tér nagyobb, mint a dielektrikum átütési szilárdsága. A legnagyobb tér a dielektrikumban a henger felületén van. Ezért a legkisebb töltéssűrűség, ami ahhoz kell, hogy a dielektrikum átüssön:
![\[\omega_1 = \epsilon_0\cdot\epsilon_r\cdot E_{kr1}\]](/images/math/f/3/d/f3d8634a77d527fb585b1dc12dc74221.png)
Teljesen hasonlóan a legkisebb töltéssűrűség, ami ahhoz kell, hogy a levegő átüssön:
![\[\omega_2 = \epsilon_0\cdot \frac{R_2}{R_1}\cdot E_{kr2}\]](/images/math/2/0/7/2074dfcaa31794abbedd5106bfd5022d.png)
Ezért a henger felületére vihető legnagyobb töltéssűrűség:
![\[\omega = \min\left\lbrace \omega_1,\omega_2\right\rbrace\]](/images/math/5/e/3/5e3c2ed53173f9f5692b66eaf3795f14.png)