Elektrosztatika - Dielektrikumok, Gauss-tétel. Kapacitás, kondenzátorok
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Beleznai (vitalap | szerkesztései) 2018. február 23., 14:33-kor történt szerkesztése után volt.
Feladatok
- Egy síkkondenzátor dielektrikuma két rétegből áll, amelyek elválasztó felülete a fegyverzetekkel párhuzamos. Meghatározandó a kondenzátorra kapcsolható legnagyobb feszültség, ha az egyik réteg vastagsága
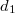 , relatív permittivitása
, relatív permittivitása 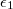 , és átütési szilárdsága
, és átütési szilárdsága 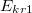 . Ugyanezek az értékek a másik rétegre:
. Ugyanezek az értékek a másik rétegre: 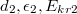 .Végeredmény
.Végeredmény![\[U = \frac{E_{kr}}{\epsilon_1} \cdot d_1 + \frac{E_{kr}}{\epsilon_2} \cdot d_2\]](/images/math/f/0/f/f0f7bb833f291f4e0429052e23cb9a23.png)
ahol![\[E_{kr} = \min\left\lbrace E_{kr1},E_{kr2}\right\rbrace \]](/images/math/6/5/8/658366583dd75fb4986ba28072f9bb00.png)
- Ideális síkkondenzátor fegyverzetei egymástól
 távolságra vannak. A kondenzátor beljesében a térerősség
távolságra vannak. A kondenzátor beljesében a térerősség 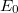 .
.
a) Hányszorosára változik meg a kondenzátor kapacitása, ha a fegyverzetekkel párhuzamosan egy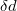 vastagságú fémlemezt helyezünk a kondenzátor belsejébe?
vastagságú fémlemezt helyezünk a kondenzátor belsejébe?
b) Rajzolja fel a térerősséget, mint a fegyverzettől mért távolság függvényét, ha a fémlemezt a baloldali fegyverzettől távolságra van.
távolságra van.
c) Rajzolja fel a potenciál változását a hely függvényében az előző összeállításnál! Mekkora a fegyverzetek közötti feszültség?
d) Milyen vastag a szigetelőlemez hatására változik a síkkondenzátor kapacitása ugyanannyiszorosára, mint a fémlemez esetében, ha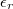 adott?Végeredménya)
adott?Végeredménya)![\[\frac{C_1}{C_0} = \frac{\frac{Q}{U_1}}{\frac{Q}{U_0}} = \frac{U_0}{U_1} = \frac{d}{d-\delta d}\]](/images/math/d/f/6/df6ebefccd82ebee28c598d862fd6025.png)
b) A térerősség a kondenzátorban konstans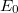 , kivéve a fémben, ahol zérus.
, kivéve a fémben, ahol zérus.
c) A pontenciál a fegyverzetek között lineárisan növekszik, kivéve a fémben, ahol konstans értéket vesz fel.
d)![\[U_2 = E_0\cdot\left(d-\delta d_2+\frac{\delta d_2}{\epsilon_r}\right)\]](/images/math/5/c/7/5c734cf2918bce0aff495076d44f804f.png)
- Egy síkkondenzátor egymástól
 távolságra lévő fegyverzetei között olyan dielektrikum van, amelynek relatív permittivitása lineárisan változik 1-től 2-ig. A töltéssűrűség abszolút értéke a lemezeken
távolságra lévő fegyverzetei között olyan dielektrikum van, amelynek relatív permittivitása lineárisan változik 1-től 2-ig. A töltéssűrűség abszolút értéke a lemezeken  . Mekkora a feszültség a két fegyverzet között?ÚtmutatásIntegráljuk a térerősséget a lemezek közötti szakaszonVégeredmény
. Mekkora a feszültség a két fegyverzet között?ÚtmutatásIntegráljuk a térerősséget a lemezek közötti szakaszonVégeredmény![\[U = \int_0^d E\cdot dx =\int_0^d \frac{\omega}{\left(1+\frac{x}{d}\right)\cdot\epsilon_0} dx = \frac{\omega}{\epsilon_0}\cdot d\cdot\ln(2)\]](/images/math/d/1/e/d1efdfa66a34b16c23fb8de843770e0e.png)
- Egy
 sugarú, végtelen hosszú fémhenger felületi töltéssűrűségre
sugarú, végtelen hosszú fémhenger felületi töltéssűrűségre  . A felületet egyenletes
. A felületet egyenletes  vastagságú,
vastagságú, 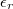 permittivitású réteggel vesszük körül.
permittivitású réteggel vesszük körül.
a) Mekkora a henger felületi töltéssűrűsége, ha egy töltést
töltést 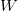 munka árán tudunk a henger tengelyétől
munka árán tudunk a henger tengelyétől 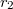 távolságból
távolságból 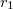 távolságba hozni.
távolságba hozni. ![\[r_2 > R_1+d > r_1 \]](/images/math/4/2/0/420587a481ef7c00f3b9ebcdab045e2b.png)
b) Ábrázoljuk, hogyan változik a térerősség a tengelytől mért távolság függvényében!
c) Mekkora maximális töltéssűrűség vihető a henger felületére, ha a dielektrikum átütési szilárdsága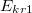 , a levegőé pedig
, a levegőé pedig 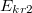 ?Végeredménya)
?Végeredménya)![\[\omega = \frac{W\cdot \epsilon_0}{R_1\cdot q \cdot \ln\left(\left(\frac{r_1}{R_2}\right)^{\frac{1}{\epsilon_r}}\cdot\frac{R_2}{r_2}\right)}\]](/images/math/a/0/1/a017c9bac5ffea60759e3f2318896539.png)
c) A legkisebb töltéssűrűség ami ahhoz kell, hogy a dielektrikum átüssön:![\[\omega_1 = \epsilon_0\cdot\epsilon_r\cdot E_{kr1}\]](/images/math/f/3/d/f3d8634a77d527fb585b1dc12dc74221.png)
Teljesen hasonlóan a legkisebb töltéssűrűség ami ahhoz kell, hogy a levegő átüssön:![\[\omega_2 = \epsilon_0\cdot \frac{R_2}{R_1}\cdot E_{kr2}\]](/images/math/2/0/7/2074dfcaa31794abbedd5106bfd5022d.png)
Ezért a henger felületére vihető legnagyobb töltéssűrűség:![\[\omega = \min\left\lbrace \omega_1,\omega_2\right\rbrace\]](/images/math/5/e/3/5e3c2ed53173f9f5692b66eaf3795f14.png)
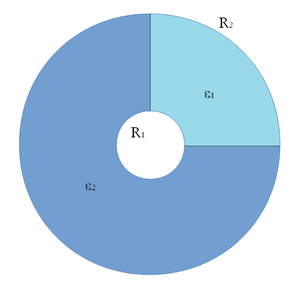
- Végtelen hosszú hengerkondenzátorban kétféle szigetelő anyag van az ábrán látható módon elrendezve. A hengerkondenzátor fegyverzeteinek sugara
 és
és  ,
,  hosszúságú szakaszon a töltésük
hosszúságú szakaszon a töltésük 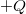 és
és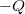 . A szigetelők relatív permittivitása
. A szigetelők relatív permittivitása 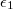 és
és 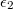 .
.
a) Írja fel az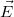 térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
térerősség vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
b) Írja fel a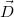 elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
elektromos eltolás vektor nagyságát, mint a sugár függvényét mindkét szigetelőben!
c) Határozza meg a hosszúságú szakasz kapacitását!
hosszúságú szakasz kapacitását!
d) Mekkora lehet a töltés, ha kondenzátorban használt szigetelő anyagok (
töltés, ha kondenzátorban használt szigetelő anyagok (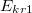 illetve
illetve 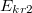 ) kritikus felett átütnek, és elveszítik szigetelő tulajdonságukat?
) kritikus felett átütnek, és elveszítik szigetelő tulajdonságukat?
Végeredménya)![\[\vec{E} = \frac{Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right) \]](/images/math/2/4/a/24a3abdf5a295a6cfbb2ec7f3835160e.png)
b)![\[\vec{D_1} = \epsilon_1\cdot\vec{E} = \frac{\epsilon_1 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)\]](/images/math/2/c/f/2cfbef7474bcbd37550e06bbd634d18e.png)
![\[\vec{D_2} = \epsilon_2\cdot\vec{E} = \frac{\epsilon_2 Q}{2\pi l r \epsilon_0}\cdot\left(\frac{1}{\frac{\epsilon_1}{4}+\frac{3\epsilon_2}{4}} \right)\]](/images/math/d/4/b/d4bc9a8ac76e4235127eb78c73b0ab1f.png)
c)d)![\[C = \frac{Q}{U} = \frac{\pi\epsilon_0 l\cdot\left(\epsilon_1+3\epsilon_2\right)}{2\cdot\ln\left(\frac{R_2}{R_1}\right)}\]](/images/math/d/9/f/d9f9666b26fd1fc99847d2cfa664a918.png)
![\[Q_{max} = 2 E_{kr} \pi l R_1\epsilon_0\cdot\left(\frac{3\epsilon_2}{4}+\frac{\epsilon_1}{4}\right)\]](/images/math/7/5/6/7568cc9135352f16688c33daad9d0fe6.png)
ahol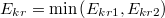
- Az
 és az
és az  sugarú koncentrikus gömb közötti térrészt inhomogén szigetelő tölt ki, amelynek permittivitása a közös centrumtól mért távolság függvénye. Milyen függvény szerint kell változnia a permittivitásnak, hogy a kondenzátort feltöltve az elektromos térerősség nagysága az egész térrészben állandó legyen? Számítsuk ki ezen kondenzátor kapacitását!ÚtmutatásA Gauss tétel segítségével számoljuk ki az elektromos teret és integráljuk a távolság függvényébenVégeredmény
sugarú koncentrikus gömb közötti térrészt inhomogén szigetelő tölt ki, amelynek permittivitása a közös centrumtól mért távolság függvénye. Milyen függvény szerint kell változnia a permittivitásnak, hogy a kondenzátort feltöltve az elektromos térerősség nagysága az egész térrészben állandó legyen? Számítsuk ki ezen kondenzátor kapacitását!ÚtmutatásA Gauss tétel segítségével számoljuk ki az elektromos teret és integráljuk a távolság függvényébenVégeredmény![\[C = \frac{4\pi\epsilon_0\alpha}{R-r}\]](/images/math/1/f/c/1fc8e2bb621672b1620472c6e78854dc.png)
- Egy síkkondenzátor
 területű fegyverzeti egymástól
területű fegyverzeti egymástól  távolságra vannak. A fegyverzetek közötti teret egy
távolságra vannak. A fegyverzetek közötti teret egy  relatív dielektromos állandójú szigetelő tölti ki. Mennyi munkát végzünk, amikor teljesen kihúzzuk a lemezet a kondenzátor fegyverzeti közül, ha
relatív dielektromos állandójú szigetelő tölti ki. Mennyi munkát végzünk, amikor teljesen kihúzzuk a lemezet a kondenzátor fegyverzeti közül, ha
a) a lemezek töltése állandó?
töltése állandó?
b) a lemezek közti feszültség állandó?
feszültség állandó?
ÚtmutatásA munkavégzést a kondenzátor két állapotának energiakülönbségéből számoljuk ki!Végeredménya)![\[\Delta E = \frac{1}{2} Q^2\cdot\left(\frac{1}{C_2}-\frac{1}{C_1}\right) = \frac{Q^2 d}{2 A \epsilon_0}\cdot\left(1-\frac{1}{\epsilon}\right) \]](/images/math/2/8/5/2858c20c2b8f2ad9a47652da28375edb.png)
b)![\[\Delta E = \frac{1}{2} U^2\cdot\left(C_2-C_1\right) = \frac{U^2 A \epsilon_0}{2 d }\cdot\left(\epsilon-1\right) \]](/images/math/e/d/8/ed8eea9d72b1df5d57873055310cb9c4.png)
- Adott egy síkkondenzátor, melynek fegyverzetei egymástól
 távolságra helyezkednek el. A kondenzátort feltekerjük egy vastag,
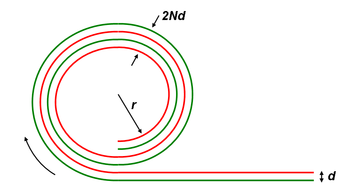
távolságra helyezkednek el. A kondenzátort feltekerjük egy vastag,  sugarú hengerre úgy, hogy annak palástján a fegyverzetek
sugarú hengerre úgy, hogy annak palástján a fegyverzetek  réteget alkotnak az 1. ábra szerint. Mennyivel változik az így kapott kondenzátor kapacitása az eredeti állapotához képest? Tételezzük fel, hogy a feltekert fegyverzetek sok réteget alkotnak (
réteget alkotnak az 1. ábra szerint. Mennyivel változik az így kapott kondenzátor kapacitása az eredeti állapotához képest? Tételezzük fel, hogy a feltekert fegyverzetek sok réteget alkotnak (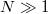 ), és a rétegrendszer teljes vastagsága lényegesen kisebb, mint a henger sugara (
), és a rétegrendszer teljes vastagsága lényegesen kisebb, mint a henger sugara (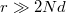 ).
).
1. ábraÚtmutatásA Gauss tétel segítségével állapítsuk meg az egyes fóliarétegeken lévő töltésmennyiséget és adjuk össze!Végeredmény![\[C=\dfrac{Q}{U}=\dfrac{\dfrac{2N-1}{N}A\varepsilon_{0}E}{Ed}=\dfrac{2N-1}{N}\varepsilon_{0}\dfrac{A}{d} \]](/images/math/b/4/0/b407bccfa069329440f1af6e284f3724.png)