Mechanika - Forgó henger lejtőn húzva
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Merev testek II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*3.3.18.)
 sugarú,
sugarú,  tömegű homogén körhenger kerületére fonalat csavarunk. A hengert ezután
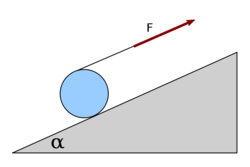
tömegű homogén körhenger kerületére fonalat csavarunk. A hengert ezután  hajlásszögű lejtőre helyezzük. A hengert elengedve a fonalat
hajlásszögű lejtőre helyezzük. A hengert elengedve a fonalat  erővel húzzuk felfelé. Mekkora kötélerő biztosítja azt, hogy a henger csak forgó mozgást végezzen?
erővel húzzuk felfelé. Mekkora kötélerő biztosítja azt, hogy a henger csak forgó mozgást végezzen?
Megoldás
Ha a henger csak forgómozgást végez, akkor a felülete a lejtőn csúszik, valamint tömegközéppontja nem gyorsul. A mozgásegyenletek:![\[ma=mg\sin{\alpha}-\mu mg\cos{\alpha}-F=0\]](/images/math/7/b/1/7b12bea5b841c45eb424b65977ccb9c0.png)
![\[\theta\beta=FR-\mu mg\cos{\alpha}R\]](/images/math/2/e/d/2ed9a559dbf41391d08819b835eb0905.png)
![\[F=mg\sin{\alpha}-\mu mg\cos{\alpha}>0,\]](/images/math/9/4/0/9402d23564cc09a502f06f5768d5174d.png)
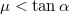 . Ezt felhasználva a második egyenletből pedig
. Ezt felhasználva a második egyenletből pedig ![\[\beta=\frac{2g}R(\sin{\alpha}-2\mu\cos{\alpha}),\]](/images/math/b/a/2/ba2ac9170f2a211a78bbb7b3200af353.png)