Magnetosztatika - Erőhatások mágneses térben
A Fizipedia wikiből
Feladatok
- Egy
 sugarú,
sugarú,  áram által átjárt körvezetőt síkjára merőleges
áram által átjárt körvezetőt síkjára merőleges  indukciójú homogén mágneses térbe helyezünk. Mekkora és milyen irányú erő hat a félkör hosszúságú vezető darabra?
indukciójú homogén mágneses térbe helyezünk. Mekkora és milyen irányú erő hat a félkör hosszúságú vezető darabra?
- Egy hurok alakú vezeték két végtelen hosszúnak tekintett
 tengellyel párhuzamos egyenes szakaszból és egy
tengellyel párhuzamos egyenes szakaszból és egy  sugarú félkörből áll. A vezetékben
sugarú félkörből áll. A vezetékben 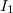 erősségű áram folyik. Egy másik egyenes vezető az első egyenes szakaszaival egy síkban, az
erősségű áram folyik. Egy másik egyenes vezető az első egyenes szakaszaival egy síkban, az  tengellyel párhuzamosan, a félkör középpontjától
tengellyel párhuzamosan, a félkör középpontjától 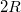 távolságra helyezkedik el. Ebben a második vezetőben
távolságra helyezkedik el. Ebben a második vezetőben 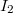 áramerősségű áram folyik. Mekkora erőt fejt ki az
áramerősségű áram folyik. Mekkora erőt fejt ki az 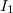 árammal átjárt egyenes vezető a hurok alakúra?
árammal átjárt egyenes vezető a hurok alakúra?
- Egy
 hosszúságú vezető darabból egy négyzet alakú, majd más alkalommal egy kör alakú hurkot készítünk, és mindkét esetben
hosszúságú vezető darabból egy négyzet alakú, majd más alkalommal egy kör alakú hurkot készítünk, és mindkét esetben  indukciójú homogén mágneses térbe helyezzük. A keret síkja mindegyik esetben
indukciójú homogén mágneses térbe helyezzük. A keret síkja mindegyik esetben 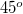 -os szöget zár be a mágneses erőtérrel, a keretben pedig
-os szöget zár be a mágneses erőtérrel, a keretben pedig  erősségű áram folyik. Határozzuk meg a keretre ható forgatónyomatékot mindkét esetben.
erősségű áram folyik. Határozzuk meg a keretre ható forgatónyomatékot mindkét esetben.
- Egy végtelen vonalvezető és egy
 szélességű végtelen szalag egy síkban, párhuzamosan fekszik. A vonalvezető és a szalag közelebbi éle
szélességű végtelen szalag egy síkban, párhuzamosan fekszik. A vonalvezető és a szalag közelebbi éle  távolságra van egymástól. A vonalvezetőben
távolságra van egymástól. A vonalvezetőben 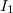 , a szalagban ugyanilyen irányú
, a szalagban ugyanilyen irányú 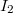 áram folyik. A szalagban az áramsűrűség homogén. Mekkora az egységnyi hosszra jutó vonzóerő a két vezető között?
áram folyik. A szalagban az áramsűrűség homogén. Mekkora az egységnyi hosszra jutó vonzóerő a két vezető között?
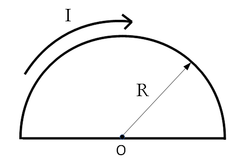
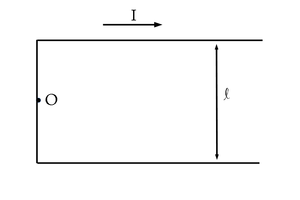
- Az ábrán látható két elrendezésnél mekkora az
 pont körüli nagyon kis
pont körüli nagyon kis 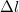 szakaszra ható erő, ha az áramerősség
szakaszra ható erő, ha az áramerősség  ?
?
a) az a.) ábrán a kör sugara
b) a b.) ábrán a párhuzamos vezetékek igen hosszúak, távolságuk
- Határozzuk meg a mágneses dipólusmomentumát egy kör alakú áramhuroknak, ha a sugara
 és a középpontjában a mágneses indukció nagysága
és a középpontjában a mágneses indukció nagysága  !
!
- Két egymással párhuzamos, elhanyagolható ellenállású, hosszú egyenes vezeték egyik végéhez
 ellenállást, másik végéhez telepet csatlakoztatunk. A hengeres vezetékek sugara
ellenállást, másik végéhez telepet csatlakoztatunk. A hengeres vezetékek sugara  , tengelyük távolsága
, tengelyük távolsága  . (
. (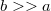 ) Mekkora
) Mekkora  ellenállásnál lesz a vezetékre ható eredő erő zérus?
ellenállásnál lesz a vezetékre ható eredő erő zérus?
![\[F_y=\int dF_y=IBR \int_0^{\pi} \sin(\varphi)d\varphi=-IBR(\cos(\pi)-\cos(0))=2IBR\]](/images/math/1/9/4/1941b9766799467bd9482f7e768a98bb.png)
![\[F_x=\int dF_x= \dfrac{\mu_0 I_1 I_2}{2 \pi } \int_{-\pi}^{\pi}\dfrac{\cos(\varphi)}{(2-\cos(\varphi))} d\varphi\]](/images/math/6/f/e/6fe2e134499f687acc2f2ff2859376ca.png)
![\[M_1=IA_1B \sin(45^o)=I\dfrac{l^2B \sqrt{2}}{32}\]](/images/math/c/a/e/cae0be15ce4fb981cf79f9ce17fb7952.png)
![\[M_2=IA_2B \sin(45^o)=I\dfrac{l^2B \sqrt{2}}{8\pi}\]](/images/math/0/0/1/001b87322df4da81aab4ffb520410570.png)
![\[F=\int dF=\dfrac{\mu_0 I_1 I_2l}{2\pi b} \int_a^{a+b} \dfrac{1}{r}dr=\dfrac{\mu_0 I_1 I_2l}{2\pi b} \ln\left( \dfrac{a+b}{a} \right)\]](/images/math/7/3/a/73ad60c7713bd120571abd3fe3e32822.png)
![\[F=\dfrac{\mu_0 I^2 \Delta l}{4 R}\]](/images/math/7/6/e/76e1f10cb04de136ae533250131b5c97.png)
![\[\vec{F}=2B_1 I \Delta l=\dfrac{\mu_0 I^2 \Delta l}{ \pi l}\]](/images/math/2/a/e/2aef22b93f810ec6a26fe469ee945c7d.png)
![\[M=IA=\dfrac{2BR}{\mu_0}R^2 \pi=\dfrac{2\pi BR^3}{\mu_0}\]](/images/math/0/6/c/06cabe809e7f09bd33fcabda284fb8d4.png)
![\[R=\dfrac{1}{\pi}\sqrt{ \dfrac{\mu_0}{\varepsilon_0} } \ln \left( \dfrac{b-a}{a} \right) \]](/images/math/d/d/2/dd2b526116ec1a2563c1a54035b2c5f4.png)