Magnetosztatika példák - Végtelen vonalvezető és szalagvezető közötti mágneses erőhatás

Feladat

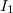1. Egy végtelen vonalvezető és egy $\setbox0\hbox{$b$}% \message{//depth:\the\dp0//}% \box0%$ szélességű végtelen szalag egy síkban, párhuzamosan fekszik. A vonalvezető és a szalag közelebbi éle $\setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0%$ távolságra van egymástól. A vonalvezetőben $\setbox0\hbox{$I_1$}% \message{//depth:\the\dp0//}% \box0%$, a szalagban ugyanilyen irányú 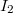$\setbox0\hbox{$I_2$}% \message{//depth:\the\dp0//}% \box0%$ áram folyik. A szalagban az áramsűrűség homogén. Mekkora az egységnyi hosszra jutó vonzóerő a két vezető között?

Megoldás

Az Egyenes vezető mágneses tere feladatából tudjuk, hogy az 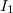$\setbox0\hbox{$I_1$}% \message{//depth:\the\dp0//}% \box0%$ árammal átjárt végtelen vonalvezető mágneses tere a következő:

$\[B(r)=\dfrac{\mu_0 I_1}{2 \pi r}\]$

Ebben az inhomogén mágneses térben helyezkedik el a vezető szalag, melyet képzeletben elemi 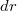$\setbox0\hbox{$dr$}% \message{//depth:\the\dp0//}% \box0%$ szélességű csíkokra bontunk. Az egyes csíkok $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ távolságra vannak a vonalvezetőtől. Az egy elemi csíkban folyó áram erőssége:

$\[dI=I_2\dfrac{dr}{b}\]$

Ezek alapján már meghatározhatjuk az $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú elemi csíkra ható infinitezimális Lorentz erőt:

$\[dF=lB(r)dI=\dfrac{I_2lB(r)}{b}dr\]$

A Lorentz erő eredeti összefüggésében szereplő 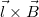$\setbox0\hbox{$\vec{l}\times \vec{B}$}% \message{//depth:\the\dp0//}% \box0%$ vektorszorzat azért egyszerűsíthető a mennyiségek nagyságának szorzatával, mert itt a mágneses tér merőleges az elemi vezetékek irányára. A Lorentz erő iránya a vonalvezető felé mutat. Az elemi Lorentz erő fenti egyenletébe behelyettesítjük az inhomogén tér helyfüggését:

$\[dF=\dfrac{\mu_0 I_1 I_2l}{2\pi b r}dr\]$

Ha a teljes szalagra ható erőt meg akarjuk határozni, Az elemi Lorentz erőket fel kell összegezni a szalag $\setbox0\hbox{$b$}% \message{//depth:\the\dp0//}% \box0%$ szélessége mentén:

$\[F=\int dF=\dfrac{\mu_0 I_1 I_2l}{2\pi b} \int_a^{a+b} \dfrac{1}{r}dr=\dfrac{\mu_0 I_1 I_2l}{2\pi b} \ln\left( \dfrac{a+b}{a} \right)\]$