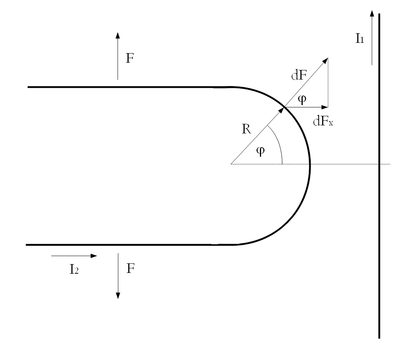
Magnetosztatika példák - Hurok és egyenes alakú áramvezető közötti mágneses erőhatás

Feladat

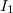1. Egy hurok alakú vezeték két végtelen hosszúnak tekintett $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ tengellyel párhuzamos egyenes szakaszból és egy $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$ sugarú félkörből áll. A vezetékben $\setbox0\hbox{$I_1$}% \message{//depth:\the\dp0//}% \box0%$ erősségű áram folyik. 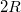Egy másik egyenes vezető az első egyenes szakaszaival egy síkban, az $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ tengellyel párhuzamosan, a félkör középpontjától $\setbox0\hbox{$2R$}% \message{//depth:\the\dp0//}% \box0%$ távolságra helyezkedik el. Ebben a második vezetőben 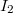$\setbox0\hbox{$I_2$}% \message{//depth:\the\dp0//}% \box0%$ áramerősségű áram folyik. Mekkora erőt fejt ki az 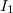$\setbox0\hbox{$I_1$}% \message{//depth:\the\dp0//}% \box0%$ árammal átjárt egyenes vezető a hurok alakúra?

Megoldás

Az Egyenes vezető mágneses tere 2 feladata alapján tudjuk, hogy a végtelen hosszú, 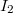$\setbox0\hbox{$I_2$}% \message{//depth:\the\dp0//}% \box0%$ árammal átjárt egyenes vezető mágneses tere:

$\[B(r)=\dfrac{\mu_0 I_1}{2 \pi r}\]$

Ebben az inhomogén mágneses térben van elhelyezve az 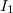$\setbox0\hbox{$I_1$}% \message{//depth:\the\dp0//}% \box0%$ árammal átjárt hurok, melyre ható erőt a hurok elemi $\setbox0\hbox{$dl$}% \message{//depth:\the\dp0//}% \box0%$ vezetékdarabjaira ható

$\[\vec{dF}=I_1(\vec{dl}\times \vec{B(r)})\]$

Lorentz erők összegzésével határozhatunk meg.

Az ábra segítségével és a Lorentz erő összefüggése alapján észrevehetjük, hogy a hurok alakú vezető egyenes szakaszaira ellentétes irányú, de azonos nagyságú Lorentz erő hat, hiszen ugyanazon mágneses térben van elhelyezve két egyforma félegyenes, melyekben ellentétes irányú áram folyik. A hurokra ható eredő erő tehát megegyezik a félkörre ható Lorentz erővel. A félkör alakú vezetékdarabot parametrizáljuk a kör $\setbox0\hbox{$\varphi$}% \message{//depth:\the\dp0//}% \box0%$ középponti szögével, mely megadja, hogy a félkör adott pontjához húzott sugár mekkora szöget zár be az $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ tengellyel. Ez alapján egy 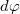$\setbox0\hbox{$d\varphi$}% \message{//depth:\the\dp0//}% \box0%$ szög alatt látszódó infinitezimális $\setbox0\hbox{$dl$}% \message{//depth:\the\dp0//}% \box0%$ ívelem hossza:

$\[dl=Rd\varphi\]$

Továbbá az adott pont 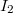$\setbox0\hbox{$I_2$}% \message{//depth:\the\dp0//}% \box0%$ árammal átjárt vezetőtől mért távolsága:

$\[r=2R-R\cos(\varphi)=R(2-\cos(\varphi))\]$

A $\setbox0\hbox{$dl$}% \message{//depth:\the\dp0//}% \box0%$ elemi ívdarabra ható Lorentz erő nagysága:

$\[dF=I_1 B(r)dl=I_1 B(r)Rd\varphi\]$

Iránya pedig minden pontban sugár irányú. Mivel a hurok szimmetrikus az $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ tengelyre, feltételezhetjük, hogy az elemi Lorentz erők $\setbox0\hbox{$y$}% \message{//depth:\the\dp0//}% \box0%$ komponensei kioltják egymást, míg az $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ komponensei konstruktívan összegződnek. Adott elemi Lorentz erő $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ itányú komponense felírható a következőképp:

$\[dF_x=dF\cos(\varphi)=I_1 B(r) R\cos(\varphi) d\varphi\]$

Behelyettesítve az összefüggésbe a mágneses tér helyfüggését:

$\[dF_x=I_1 \dfrac{\mu_0 I_2}{2 \pi r}R\cos(\varphi) d\varphi\]$

Majd az elemi ívdarab egyenes vezetőtől mért $\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%$ távolságának $\setbox0\hbox{$\varphi$}% \message{//depth:\the\dp0//}% \box0%$ függvényét figyelembe véve:

$\[dF_x=I_1 \dfrac{\mu_0 I_2}{2 \pi R(2-\cos(\varphi))}R\cos(\varphi) d\varphi\]$

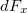A teljes félkörre ható $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ irányú erőt megkaphatjuk, ha az elemi $\setbox0\hbox{$dF_x$}% \message{//depth:\the\dp0//}% \box0%$ erőket felösszegezzük a 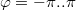$\setbox0\hbox{$\varphi=-\pi..\pi$}% \message{//depth:\the\dp0//}% \box0%$ félkörív mentén:

$\[F_x=\int dF_x= \dfrac{\mu_0 I_1 I_2}{2 \pi } \int_{-\pi}^{\pi}\dfrac{\cos(\varphi)}{(2-\cos(\varphi))} d\varphi\]$

Az integrál kiszámítását helyettesítéses módszerrel tudjuk elvégezni megfelelő átalakítások után, ugyanakkor a helyettesítés nem triviális és az integrálás elvégzése időigényes, ezért ezt itt nem prezentáljuk.