Magnetosztatika példák - Küllős fémtárcsában indukált elektromotoros erő
A Fizipedia wikiből
Feladat
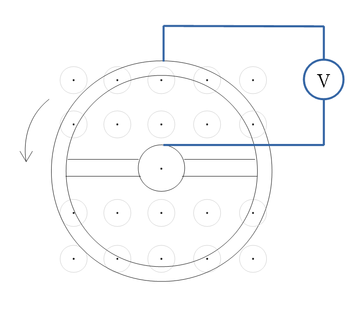
- Küllős fémtárcsát forgassunk homogén mágneses erőtérben az erővonalakkal párhuzamos tengely körül. Mekkora feszültség mérhető a tárcsa tengelye és pereme között? A tárcsa sugara
 , a mágneses indukció
, a mágneses indukció  a fordulatszám
a fordulatszám  .
.
Megoldás
A kerékkel együtt forgó elektronokra a mágneses tér miatt Lorentz erő hat.
![\[\vec{F_L} = q\left(\vec{B}\times \vec{v}\right)\]](/images/math/9/1/0/91020ecdcefb3365c0a37762197031e4.png)
A Lorentz erő hatására töltés átrendeződés megy végbe, aminek eredményeképpen a kerékben kialakul egy elektromos tér. A stacionárius egyensúly beállta után a töltésmegosztás következtében kialakult sztatikus elektromos tér és a Lorentz erő következtében fellépett kioltják egymást:
![\[q\vec{E} = q\left(\vec{B}\times \vec{v}\right) \]](/images/math/4/7/e/47e4e5f526f3530125178ece3f28c744.png)
Az elektronok sebessége a középpontól mért  távolságban:
távolságban: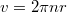 Mivel a mágneses tér mindenütt merőleges az elektronok sebességére ezért:
Mivel a mágneses tér mindenütt merőleges az elektronok sebességére ezért:
![\[E = 2\pi n r B\]](/images/math/8/5/5/85549b372f183e8bad01ef0399ef94fe.png)
A tárcsa tengelye és pereme között mérhető feszültség:
![\[U = \int_0^R E dr = \frac{2\pi n B R^2}{2} \]](/images/math/7/9/8/7989c4762bee70f7e0422e10dde85dd2.png)