Munka, energia - Munka számítás 1
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Munka, energia |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy síkon mozgó tömegpontra az alábbi általánosított rugalmas erő hat: ahol az általánosított rugalmas állandók:
![\[F_x(x,y) = - A \, x - B \, y \qquad F_y(x,y) = - B \, x - C \, y \; ,\]](/images/math/5/a/4/5a4b48e52b0269e183591efc8a11e15f.png)
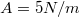 ,
, 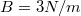 és
és 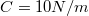 . A tömegpont az origóból indulva, az
. A tömegpont az origóból indulva, az  tengellyel
tengellyel 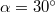 szöget bezáró egyenes pályán mozog.
szöget bezáró egyenes pályán mozog.
- a.) Adjuk meg a rugalmas erő
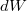 elemi munkáját, amíg a test távolsága az origótól
elemi munkáját, amíg a test távolsága az origótól  -ről
-ről 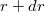 -re változik.
-re változik.
- b.) Ez alapján számítsuk ki, mennyi munkát végez a rugalmas erő, amíg a tömegpont az origótól
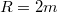 távolságra jut!
távolságra jut!
- c.) (Bónusz kérdés): Hogyan tudunk ilyen "általánosított" rugóerőt létrehozni?
- a.) Adjuk meg a rugalmas erő
Megoldás
- a.) Amikor a tömegpont
 távolságra van, akkor a helyvektorának koordinátái
távolságra van, akkor a helyvektorának koordinátái 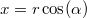 ,
, 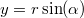 . A kicsiny elmozdulásvektor koordinátái pedig
. A kicsiny elmozdulásvektor koordinátái pedig 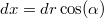 és
és  .
.
- A rugalmas erő komponensei pedig Az elemi munka az erővektor és a kicsiny elmozdulásvektor skaláris szorzata:
![\[F_x = - A \,r \cos(\alpha) - B \, r \sin(\alpha) \qquad F_y = - B \, r \cos(\alpha) - C \, r \sin(\alpha) \; .\]](/images/math/0/a/2/0a2c39edaa983c3d55ba3df18d3f2582.png)
![\[dW = \vec{F} \cdot d\vec{r} = F_x \, dx + F_y \, dy = - A \cos^2(\alpha) \, r dr - B \sin(\alpha) \cos(\alpha) \, r dr - B \cos(\alpha) \sin(\alpha) \, r dr - C \sin^2(\alpha) \, r dr \, .\]](/images/math/3/0/2/302ba95a1f56f243c243f47d0e201413.png)
- b.) A teljes munkavégzés:
![\[ W = \int dW = \int_0^R (-A \cos^2(\alpha) - 2 B \sin(\alpha) \cos(\alpha) - C \sin^2(\alpha)) \, r \, dr = - (A \cos^2(\alpha) + 2 B \sin(\alpha) \cos(\alpha) + C \sin^2(\alpha)) \frac{R^2}{2}\]](/images/math/5/3/2/532aa381dc7b53df251564b8889e1030.png)
- c.) Vegyük észre, hogy az erő és az elmozdulás vektorok között lineáris az összefüggés: A rugóállandó egy szimmetrikus mátrix, melynek sajátvektorai egymásra merőlegesek. A sajátértékek adják meg az adott sajátvektorhoz tartozó rugóállandót, ezek általában nem lesznek egyformák. Tehát különböző rugóállandójú, egymásra merőleges, de nem
![\[\vec{F} = - \left( \begin{array}{cc} A & B \\ B & C \end{array} \right) \vec{r} \, .\]](/images/math/5/e/7/5e7b97b2964b9f080fbf5be71d60733c.png)
 és
és  irányú rugókkal elérhető ez az általánosított eset.
irányú rugókkal elérhető ez az általánosított eset.
- a.) Amikor a tömegpont