Mechanika - Munka, energia
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Munka, energia |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- (2.2.1) Egy gépkocsi tömege
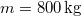 . Indulás után
. Indulás után 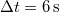 ideig gyorsít
ideig gyorsít 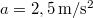 gyorsulással. Mekkora az átlagteljesítmény a
gyorsulással. Mekkora az átlagteljesítmény a  idő alatt? Írjuk fel a pillanatnyi teljesítményt, mint az idő függvényét! Számítsuk ki a teljesítmény legnagyobb értékét! (A súrlódástól eltekintünk.)
idő alatt? Írjuk fel a pillanatnyi teljesítményt, mint az idő függvényét! Számítsuk ki a teljesítmény legnagyobb értékét! (A súrlódástól eltekintünk.)
- (2.2.3) Az
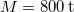 tömegű vasúti szerelvény
tömegű vasúti szerelvény 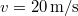 sebességgel halad, amikor leveszik a gőzt. A gördülési súrlódási együttható
sebességgel halad, amikor leveszik a gőzt. A gördülési súrlódási együttható 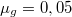 . Mekkora munkát végez az ellenállási erő a teljes megállásig, és hogyan változik a teljesítménye az időben? Mekkora úton és mennyi idő eltelte után áll meg a szerelvény?
. Mekkora munkát végez az ellenállási erő a teljes megállásig, és hogyan változik a teljesítménye az időben? Mekkora úton és mennyi idő eltelte után áll meg a szerelvény?
- (2.2.7) Egy rugót
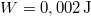 munka árán tudunk
munka árán tudunk 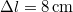 -rel megnyújtani. Mekkorának adódik a rezgésidő, ha egy
-rel megnyújtani. Mekkorának adódik a rezgésidő, ha egy 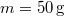 tömegű testet a végéhez erősítünk?
tömegű testet a végéhez erősítünk?
- (*2.2.9) Egy
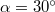 -os hajlásszögű lejtőre húzunk fel egy
-os hajlásszögű lejtőre húzunk fel egy 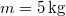 tömegű testet, a lejtő hosszával párhuzamos erővel, állandó
tömegű testet, a lejtő hosszával párhuzamos erővel, állandó 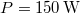 teljesítménnyel. A mozgás végig egyenletes. Milyen magasra jut fel a test
teljesítménnyel. A mozgás végig egyenletes. Milyen magasra jut fel a test 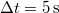 alatt? Mekkora a hatásfok? A lejtő és a test közötti súrlódási együttható
alatt? Mekkora a hatásfok? A lejtő és a test közötti súrlódási együttható 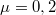 .
.
- (2.2.12) Egy
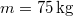 tömegű szánkó két szembenálló
tömegű szánkó két szembenálló 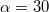 °-os hajlásszögű lejtős pályán mozog. Az egyik lejtőn elindul lefelé,
°-os hajlásszögű lejtős pályán mozog. Az egyik lejtőn elindul lefelé, 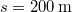 út megtétele után leért a lejtő aljára, de a kapott energia tovább viszi a másik lejtőn felfelé. Milyen hosszú utat tesz meg felfelé, ha a súrlódási együttható
út megtétele után leért a lejtő aljára, de a kapott energia tovább viszi a másik lejtőn felfelé. Milyen hosszú utat tesz meg felfelé, ha a súrlódási együttható 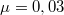 ?
?
- (*2.2.13) Egy
 magasságú
magasságú  hosszúságú lejtőt egy fém és egy falécből állítunk össze. A pálya felső részéről rövid fémhasábot eresztünk el. A fém és a fa rész hosszának milyen arányánál érjük el, hogy a hasáb a pálya végén megálljon? Mennyi időre van szükség a teljes út megtételére, ha a fémhasáb és a fém súrlódási együtthatója
hosszúságú lejtőt egy fém és egy falécből állítunk össze. A pálya felső részéről rövid fémhasábot eresztünk el. A fém és a fa rész hosszának milyen arányánál érjük el, hogy a hasáb a pálya végén megálljon? Mennyi időre van szükség a teljes út megtételére, ha a fémhasáb és a fém súrlódási együtthatója 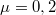 , a fémhasábé és a fáé
, a fémhasábé és a fáé 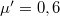 ,
, 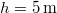 ,
, 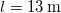 ?
?
- (*2.2.14) Egy
 tömegű testet rugalmas fonal B végére erősítünk. A fonal
tömegű testet rugalmas fonal B végére erősítünk. A fonal  vége rögzített, nyújtatlan állapotban
vége rögzített, nyújtatlan állapotban 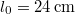 hosszúságú, és akkor tart
hosszúságú, és akkor tart 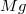 erővel egyensúlyt, ha megnyúlása
erővel egyensúlyt, ha megnyúlása 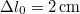 . A test kezdetben az A pontban áll, azután elengedjük, úgyhogy szabadon esik mindaddig, amíg a fonal engedi, azután a fonal elkezd nyúlni, eközben fékezi a test esését, végül meg is állítja. Tegyük fel, hogy a fonal megnyúlásával arányos erőt fejt ki a végére kötött testre. Mekkora lesz a fonal maximális megnyúlása?
. A test kezdetben az A pontban áll, azután elengedjük, úgyhogy szabadon esik mindaddig, amíg a fonal engedi, azután a fonal elkezd nyúlni, eközben fékezi a test esését, végül meg is állítja. Tegyük fel, hogy a fonal megnyúlásával arányos erőt fejt ki a végére kötött testre. Mekkora lesz a fonal maximális megnyúlása?
- (2.3.2) Egy
 tömegű test kezdősebesség nélkül igen nagy
tömegű test kezdősebesség nélkül igen nagy  magasságból esik a Földre. Mekkora a kinetikus energiája a Föld felszínére való becsapódás pillanatában? Mekkora a végsebessége, ha végtelen távolból kezdősebesség nélkül esik a Földre? A légellenállást hanyagoljuk el!
magasságból esik a Földre. Mekkora a kinetikus energiája a Föld felszínére való becsapódás pillanatában? Mekkora a végsebessége, ha végtelen távolból kezdősebesség nélkül esik a Földre? A légellenállást hanyagoljuk el!
- (*2.3.6 alapján)
- a.) Első kozmikus sebességnek nevezzük azt a sebességet, amennyivel a Föld felszínén vízszintesen el kell lőni egy testet, hogy körpályán megkerülje a Földet, feltéve hogy nincs légellenállás. Mekkora az első kozmikus sebesség a Földön?
- b.) Második kozmikus sebességnek nevezzük azt a sebességet, amennyivel elindítva egy testet a Föld felszínéről, el tud szabadulni a Földtől. Mekkora a második kozmikus sebesség?
- (Adatok:
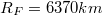 ,
, 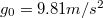 )
)
- (*2.3.11) Milyen nagyságú gravitációs vonzóerőt fejt ki egy
 hosszúságú, kis
hosszúságú, kis  keresztmetszetű,
keresztmetszetű,  sűrűségű homogén rúd a tengelyének irányában, a végpontjától
sűrűségű homogén rúd a tengelyének irányában, a végpontjától  távolságra levő
távolságra levő  tömegű tömegpontra?
tömegű tömegpontra?
- (*2.4.6) Egy
 tömegű,
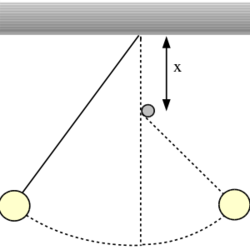
tömegű,  hosszúságú matematikai ingát vízszintes helyzetéből elengedünk. Függőleges helyzetében a kötél egy csapocskán megakad, így az inga az ábrán látható módon lendül tovább.
hosszúságú matematikai ingát vízszintes helyzetéből elengedünk. Függőleges helyzetében a kötél egy csapocskán megakad, így az inga az ábrán látható módon lendül tovább.
- a) Mi a dinamikai feltétele annak, hogy az inga további mozgása során le tudjon írni egy teljes kört?
- b) Hova kell ehhez helyezni a csapocskát?
- c) Hogyan alakul a test pályája ellenkező esetben? (szöveges válasz)
- d) Hova kell helyezni a csapocskát, hogy a c) esetben ismét az indítás magasságába jusson fel?
- Egy síkon mozgó tömegpontra az alábbi általánosított rugalmas erő hat: ahol az általánosított rugalmas állandók:
![\[F_x(x,y) = - A \, x - B \, y \qquad F_y(x,y) = - B \, x - C \, y \; ,\]](/images/math/5/a/4/5a4b48e52b0269e183591efc8a11e15f.png)
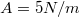 ,
, 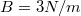 és
és 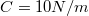 . A tömegpont az origóból indulva, az
. A tömegpont az origóból indulva, az  tengellyel
tengellyel 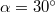 szöget bezáró egyenes pályán mozog.
szöget bezáró egyenes pályán mozog.
- a.) Adjuk meg a rugalmas erő
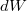 elemi munkáját, amíg a test távolsága az origótól
elemi munkáját, amíg a test távolsága az origótól  -ről
-ről 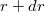 -re változik.
-re változik.
- b.) Ez alapján számítsuk ki, mennyi munkát végez a rugalmas erő, amíg a tömegpont az origótól
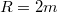 távolságra jut!
távolságra jut!
- c.) (Bónusz kérdés): Hogyan tudunk ilyen "általánosított" rugóerőt létrehozni?
- a.) Adjuk meg a rugalmas erő
- Egy
 tömegű kicsiny test egy függőleges szimmetriatengelyű parabola alakú pályán mozoghat, melynek pályaegyenlete
tömegű kicsiny test egy függőleges szimmetriatengelyű parabola alakú pályán mozoghat, melynek pályaegyenlete 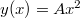 . A testre hat a nehézségi erő, a pálya súrlódásmentes. A test nulla kezdősebességgel indul a pálya
. A testre hat a nehézségi erő, a pálya súrlódásmentes. A test nulla kezdősebességgel indul a pálya 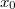 koordinátájú pontjából.
koordinátájú pontjából.
- a.) Adjuk meg a gravitációs erő elemi
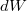 munkáját, amikor a test az
munkáját, amikor a test az  koordinátájú pontból az
koordinátájú pontból az 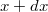 koordinátájú pontba jut.
koordinátájú pontba jut.
- b.) Adjuk meg a gravitációs erő teljes munkáját, amíg a test eljut az
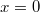 pontba!
pontba!
- c.) Munkatétel alapján adjuk meg a test sebességét az
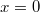 pontban!
pontban!
- a.) Adjuk meg a gravitációs erő elemi
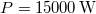
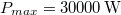
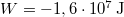
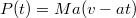
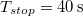
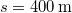
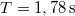
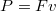 .
. 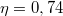
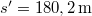
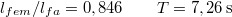
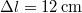
![\[E_{kin}=\gamma Mm\left(\frac{1}{R}-\frac{1}{R+h}\right) \qquad\qquad v=\sqrt{\frac{2\gamma M}{R}}\]](/images/math/6/d/f/6df2c7658d153d0f8b0027eda12dadfa.png)
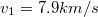
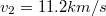
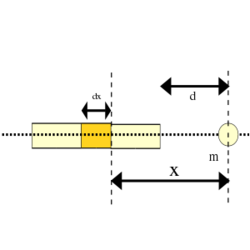
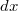 hosszúságú szakaszokra, majd ezek hatását összegezzük!
hosszúságú szakaszokra, majd ezek hatását összegezzük! ![\[F_{g}=\frac{\gamma m\rho q l}{d(d+l)}\]](/images/math/0/e/b/0eb206470686198c19f521f19bb078c9.png)
![\[0<\frac{v_{1}^{2}}{L-x}-g\]](/images/math/b/e/e/bee27b6937006c4a4891e545071800f6.png)
![\[x>\frac{3L}{5}\]](/images/math/2/8/2/282e6be4330c012f0effb2538e04d3c0.png)
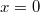
![\[ dW = - A \cos^2(\alpha) \, r dr - B \sin(\alpha) \cos(\alpha) \, r dr - B \cos(\alpha) \sin(\alpha) \, r dr - C \sin^2(\alpha) \, r dr\]](/images/math/e/4/4/e44a378d0779d07609f48a8eaac9e428.png)
![\[ W = - (A \cos^2(\alpha) + 2 B \sin(\alpha) \cos(\alpha) + C \sin^2(\alpha)) \frac{R^2}{2}\]](/images/math/1/4/d/14de301c75c5020d5755ecbd03b775db.png)
![\[dW = - 2 A m g x \, dx\]](/images/math/d/9/9/d9904f3a8a17065ca75e9348646aa2a4.png)
![\[W = m g A x_0^2\]](/images/math/d/6/7/d670ebeb15c526246e2ae8693fcc0349.png)
![\[|v_v| = \sqrt{2 g A x_0^2}\]](/images/math/8/8/d/88d9883096db0a36d364b776d9ac6ab7.png)