Termodinamika példák - Az entrópia hőmérséklet- és térfogatfüggése, az adiabata egyenlete

Feladat

1. Tekintsünk $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű, $\setbox0\hbox{$M$}% \message{//depth:\the\dp0//}% \box0%$ móltömegű, $\setbox0\hbox{$\gamma$}% \message{//depth:\the\dp0//}% \box0%$ fajhőviszonyú ideális gázt.
   • a) Vezesse le az entrópia hőmérséklet- és térfogatfüggését megadó összefüggést!
   • b) A kapott entrópia-kifejezés segítségével vezesse le az adiabata egyenletét!

Megoldás

a) Az entrópiaváltozás definíciója

$\[ \mathrm{d}S = \frac{\delta Q}{T}, \]$

amibe helyettesítsük be a közölt hő első főtételből kifejezett

$\[ \delta Q = \mathrm{d}U+p\,\mathrm{d}V \]$

alakját, ahol 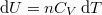$\setbox0\hbox{$ \mathrm{d}U=n C_V\,\mathrm{d}T $}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$ p=\frac{nRT}{V}$}% \message{//depth:\the\dp0//}% \box0%$:

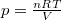$\[ \mathrm{d}S= n C_V \frac{\mathrm{d}T}{T} + nR \frac{\mathrm{d}V}{V}. \]$

Kiintegrálva az egyenletet a kezdeti- és a végállapot között:

$\[ S - S_0 = n C_V \ln\frac{T}{T_0} + nR \ln\frac{V}{V_0}, \]$

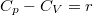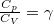ahol a fajhőösszefüggések szerint $\setbox0\hbox{$C_p-C_V=r$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\frac{C_p}{C_V}=\gamma$}% \message{//depth:\the\dp0//}% \box0%$, amikből $\setbox0\hbox{$C_V = \frac{R}{\gamma-1}$}% \message{//depth:\the\dp0//}% \box0%$:

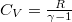$\[ S(T,V) = nR \ln\left[ \left(\frac{T}{T_0}\right)^{\textstyle \frac{1}{\gamma-1}} \frac{V}{V_0} \right] + S_0. \]$

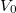Ha a hőmérsékletet és a térfogatot dimenziótlanul, $\setbox0\hbox{$T_0$}% \message{//depth:\the\dp0//}% \box0%$ illetve $\setbox0\hbox{$V_0$}% \message{//depth:\the\dp0//}% \box0%$ egységekben adjuk meg, akkor helyes a

$\[ S(T,V) = nR \ln\left[ T^{\textstyle \frac{1}{\gamma-1}} V \right] + S_0 \]$

felírás is.

b) Adiabatikus állapotváltozásban az entrópia állandó (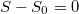$\setbox0\hbox{$S-S_0=0$}% \message{//depth:\the\dp0//}% \box0%$), azaz 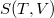$\setbox0\hbox{$S(T,V)$}% \message{//depth:\the\dp0//}% \box0%$ kifejezésében a logaritmus alatt $\setbox0\hbox{$1$}% \message{//depth:\the\dp0//}% \box0%$ áll:

$\[ \left(\frac{T}{T_0}\right)^{\textstyle \frac{1}{\gamma-1}} \frac{V}{V_0} = 1, \]$

vagyis az adiabata egyenlete

$\[ T^{\textstyle \frac{1}{\gamma-1}} V = \mathrm{const.} \]$