Termodinamika - Fajhő, Körfolyamatok
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Néhány fontos összefüggés
A Carnot-körfolyamat hatásfoka 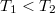 hőmérsékletű hőtartályokkal
hőmérsékletű hőtartályokkal
![\[ \eta = 1 - \frac{T_1}{T_2}, \]](/images/math/8/3/d/83dff0aeec3f5a34998f4336241a74af.png)
a hőszivattyú teljesítménytényezője 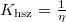 , a hűtőgép jósági tényezője
, a hűtőgép jósági tényezője 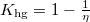 .
.
| ΔQ | ΔU | ΔW | |
| izobár p=const. |
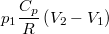
|
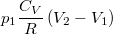
|
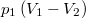
|
| izochor V=const. |
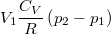
|
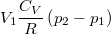
|

|
| izoterm T=const. |
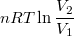
|

|
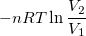
|
| adiabatikus S=const. |

|
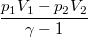
|
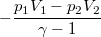
|
Feladatok
- Melegszik vagy lehűl az
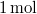 ideális gáz, ha a
ideális gáz, ha a 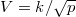 összefüggés (
összefüggés ( állandó) szerint tágul ki? Mekkora a gáz mólhője ebben a folyamatban, ha állandó térfogaton mért mólhője
állandó) szerint tágul ki? Mekkora a gáz mólhője ebben a folyamatban, ha állandó térfogaton mért mólhője 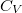 ?
?
- Határozzuk meg azon lehetséges folyamatokat megadó összefüggést, amelyek közben az ideális gáz mólhője állandó (az állandó nyomáson és állandó térfogaton mért mólhőket tekintsük ismertnek)! Vezessük le a kapott egyenletből az ismert, állandó mólhőjű speciális folyamatok egyenletét.
- Ideális gáz állapotváltozását a
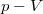 síkon a
síkon a 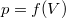 összefüggés írja le.
összefüggés írja le.
- a) Bizonyítsa be, hogy ebben a folyamatban a fajhő térfogatfüggését a összefüggés adja meg!
![\[c(V)=c_V+R\frac{f(V)}{f(V)+V\frac{\mathrm{d}f}{\mathrm{d}V}}\]](/images/math/9/5/f/95f7a48280858181d4b28ca447b3a9d2.png)
- b) Milyen
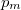 ,
, 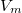 értékpárnál maximális a gáz hőmérséklete, ha az állapotváltozást a
értékpárnál maximális a gáz hőmérséklete, ha az állapotváltozást a 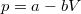 egyenlet adja meg (
egyenlet adja meg ( és
és  ismert pozitív állandók)?
ismert pozitív állandók)?
- a) Bizonyítsa be, hogy ebben a folyamatban a fajhő térfogatfüggését a
- Az első ábrán egy ideális gázzal végzett körfolyamat
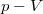 diagramja látható. Ábrázoljuk a folyamatot
diagramja látható. Ábrázoljuk a folyamatot 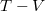 és
és 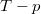 diagramon!
diagramon!
- A második ábrán egy ideális gázzal végzett körfolyamat
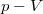 diagramja látható. Mekkora a gáz által végzett munka?
diagramja látható. Mekkora a gáz által végzett munka?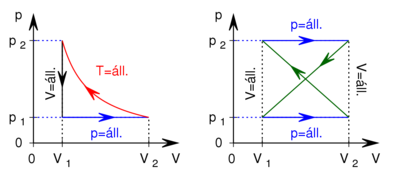
-
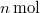 ,
, 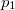 nyomású kétatomos ideális gázt
nyomású kétatomos ideális gázt 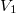 térfogatról állandó nyomáson
térfogatról állandó nyomáson 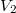 térfogatúra nyomunk össze (az ábrán 1-es út). Ezen az állandó térfogaton eredeti hőmérsékletére melegítjük (2-es út), majd izotermikusan a kiinduló térfogatára tágítjuk (3-as út).
térfogatúra nyomunk össze (az ábrán 1-es út). Ezen az állandó térfogaton eredeti hőmérsékletére melegítjük (2-es út), majd izotermikusan a kiinduló térfogatára tágítjuk (3-as út).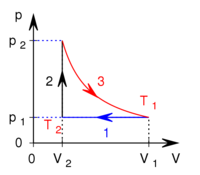
- a) Mennyivel változott a gáz belső energiája az 1-es úton?
- b) Mennyivel hőt kellet közölnünk a gázzal a 2-es úton?
- c) Mekkora a gáz által végzett munka és a gáz által felvett hő a teljes körfolyamatban?
- Egy Carnot-hűtőgép egyik hőtartályában
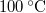 hőmérsékletű, forrásban lévő víz, a másikban
hőmérsékletű, forrásban lévő víz, a másikban 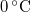 hőmérsékletű víz van. A víz forráshője
hőmérsékletű víz van. A víz forráshője 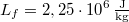 , a jég olvadáshője
, a jég olvadáshője 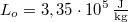 .
.
- a) Mennyi vizet kell az alsó hőtartályban
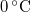 hőmérsékletű jéggé fagyasztani ahhoz, hogy a felső hőtartályban
hőmérsékletű jéggé fagyasztani ahhoz, hogy a felső hőtartályban 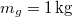 tömegű
tömegű 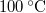 hőmérsékletű gőz keletkezzék?
hőmérsékletű gőz keletkezzék?
- b) Mennyi külső munkát kell a körfolyamatba betáplálni?
- a) Mennyi vizet kell az alsó hőtartályban
- Az ábrán a
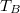 és
és 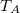 hőmérsékletekkel meghatározott körfolyamat látható. Mekkora annak a gépnek a hatásfoka, amelyik ezt a körfolyamatot mólnyi mennyiségű, adott
hőmérsékletekkel meghatározott körfolyamat látható. Mekkora annak a gépnek a hatásfoka, amelyik ezt a körfolyamatot mólnyi mennyiségű, adott  fajhőviszonyú ideális gázzal valósítja meg?
fajhőviszonyú ideális gázzal valósítja meg?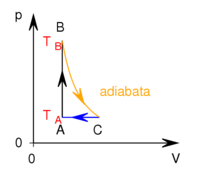
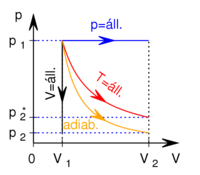
-
 mólnyi ideális gáz az ábrán látható körfolyamatot végzi. A körfolymat két izobár és két adiabata szakaszból áll, amelyeket a
mólnyi ideális gáz az ábrán látható körfolyamatot végzi. A körfolymat két izobár és két adiabata szakaszból áll, amelyeket a 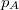 ,
, 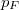 ,
, 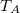 és
és 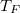 adatok határoznak meg (ez a gőzgép sémája).
adatok határoznak meg (ez a gőzgép sémája).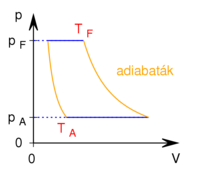
- a) Mekkora a gőzgép hatásfoka?
- b) Hogyan függ a hatásfok attól, hogy hány atomos gázmolekulákkal végezzük a körfolyamatot?
- c) Az adott gépnél és az adott gáznál hogyan növelhető a hatásfok?
- Egy épület fűtésére az ún. dinamikus fűtést használjuk:
- A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó
 hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
- A hőerőgép egy hőszivattyút működtet, amelynek alsó hőtartálya egy tó
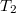 hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő
hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő  hőmérsékletű víz, amely az épületet egyúttal fűti (
hőmérsékletű víz, amely az épületet egyúttal fűti (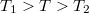 ).
).
- A tűzszekrényben
 égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül, Carnot-hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!
égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül, Carnot-hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!
- A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó
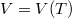 függvényt és abból a
függvényt és abból a 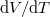 hányadost!
hányadost! ![\[C=C_V-R\]](/images/math/9/1/6/916d05fdbb5dfa7f9b35fed114625c98.png)
 -re és
-re és  -re kapott differenciálegyenletet.
-re kapott differenciálegyenletet. ![\[pV^\frac{C-C_p}{C-C_V}=\text{állandó}.\]](/images/math/0/8/4/0844c7b8571b41dceb34b69f2c02e722.png)
![\[\frac{\mathrm{d}V}{\mathrm{d}T}=\left(\frac{\mathrm{d}T}{\mathrm{d}V}\right)^{-1}\]](/images/math/c/8/8/c88d2444320e13642d1d1bc1085d8c92.png)
![\[V_m=\frac{a}{2b}\qquad\text{és}\qquad p_m=\frac{a}{2}\]](/images/math/0/4/f/04f5f3e0fd92c07431c1162d1bfa547a.png)
![\[W=0.\]](/images/math/1/5/d/15d71ac95674055e4c06112ae5313e2d.png)
![\[\Delta U_1 = p_1 \frac{V_2-V_1}{\gamma-1}, \qquad \gamma=\frac75\]](/images/math/2/f/6/2f69cad7cc3d66fb56085b61806960b8.png)
![\[\Delta Q_2=-\Delta U_1\]](/images/math/b/4/5/b45afb1d5d8899648966d216d44c756b.png)
![\[\Delta W = \Delta Q = p(V_2-V_1)+p_1V_1\ln\left(\frac{V_1}{V_2}\right)\]](/images/math/4/7/5/475bbd601cdf9182147bca5dfa9123cb.png)
![\[m_j=(1-\eta)L_f m_g/L_o=49{,}16\,\mathrm{kg},\]](/images/math/f/1/4/f147478a59f517a1b7dfabbe7bddefd5.png)
 a körfolyamat hatásfoka.
a körfolyamat hatásfoka. ![\[W=\eta L_f m_g=6{,}03\cdot 10^5\,\mathrm{J},\]](/images/math/f/5/9/f59e5efd869a9a6687ee70f425700363.png)
![\[\eta=1-\gamma\frac{x^{1/gamma}-1}{x-1},\]](/images/math/e/e/c/eec4e9f8a52e569065ee348f1a0d0fad.png)
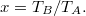
![\[\eta=1-\left(\frac{p_A}{p_F}\right)^{\frac{\gamma-1}{\gamma}}.\]](/images/math/b/0/6/b06b768320fb25e906c3a14c04833bbe.png)
![\[Q=q\frac{1-T_2/T_1}{1-T_2/T}>q.\]](/images/math/0/9/7/097b137e36faa49bbb8b3a3deaab5f04.png)