Termodinamika példák - Ideális gáz állandó mólhőjű folyamatai
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozzuk meg azon lehetséges folyamatokat megadó összefüggést, amelyek közben az ideális gáz mólhője állandó (az állandó nyomáson és állandó térfogaton mért mólhőket tekintsük ismertnek)! Vezessük le a kapott egyenletből az ismert, állandó mólhőjű speciális folyamatok egyenletét.
Megoldás
Az ideális gáz általános fajhőjére az előző feladatban bizonyítottuk, hogy
![\[ C n \mathrm{d}T = C_V n \,\mathrm{d}T + p \left(\frac{\mathrm{d} V}{\mathrm{d} T}\right)_{\substack{\text{állapot-}\\ \text{változás}}}\,\mathrm{d}T,\]](/images/math/8/f/b/8fb08a82cf552e934c172d59e1005fee.png)
küszöböljük ki a nyomást az állapotegyenlet segítségével (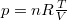 ),
),
![\[ \frac{C-C_V}{R} \frac{\mathrm{d}T}{T} = \frac{\mathrm{d}V}{V},\]](/images/math/c/8/b/c8b21e1c1438b8c835e8e223ef40c26d.png)
és integráljunk az állapotváltozás vonalán:
![\[ \frac{C-C_V}{R} \ln T = \ln V + \ln \mathrm{const.} \]](/images/math/e/1/0/e10364369ab20b2df73841117c64f134.png)
Mivel 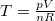 , ez
, ez
![\[ p = \mathrm{const.} \cdot V^{\textstyle \frac{R}{C-C_V}-1} = \mathrm{const.} \cdot V^{\textstyle \frac{C_p-C}{C-C_V}} \]](/images/math/b/4/9/b49f38fd48e6f74b50914ae6f1a729cb.png)
egyenletre vezet. Az állandó fajhőjű folyamatokat állandó nyomáson és térfogaton mért fajhőkkel jellemző összefüggés pedig
![\[ pV^{\textstyle \frac{C_p-C}{C_V-C}} = \mathrm{const.} \]](/images/math/8/6/5/8653911b636832843090b81a8544ce4d.png)
Megjegyzés
Ugyanerre az eredményre eljuthatunk a következő feladatban bizonyítandó
![\[ C(V) = C_V + \frac R{1+\frac V p\frac{\mathrm{d}p}{\mathrm{d}V}} \]](/images/math/c/a/3/ca32025be9a42b79ef7b81aebb654a7f.png)
öszefüggésből indulva is. Feltéve, hogy a fajhő állandó, a kifejezésben szereplő tört nevezője is állandó:
![\[ \frac V p\frac{\mathrm{d}p}{\mathrm{d}V} = A. \]](/images/math/b/3/9/b39a568f85b1a8f98d36dd5a9586e497.png)
A változókat szétválasztva és integrálva
![\[ \frac{\mathrm{d}p}{p} = A \frac{\mathrm{d}V}{V} \]](/images/math/0/9/9/0994ae27d32702461c2c70a2f7cd77ea.png)
![\[ \ln \frac p{p_0} = A \ln \frac V{V_0} \]](/images/math/1/6/e/16e24084eaf267036378b3d0f811f85b.png)
![\[ p = p_0{\left(\frac V{V_0}\right)}^A \]](/images/math/4/a/4/4a4f06e4555271db3bae36fa3e66d26f.png)
A bevezetett  állandót kifejezhetjük a
állandót kifejezhetjük a
![\[ C(V) = C_V+\frac{R}{1+A} \]](/images/math/3/b/d/3bd3ad420091395e5fb091ce1159dd15.png)
kiindulási egyenletből:
![\[A=\frac R{C-C_V}-1=\frac{C_p-C}{C-C_V}, \]](/images/math/a/2/d/a2d289509e32e25457aa71b4a8e6e5f2.png)
amivel szintén
![\[ p V^{\textstyle \frac{C-C_p}{C-C_V}} = \mathrm{const.} \]](/images/math/1/0/f/10f81b7951d90fd98a091add6406b7d4.png)