Termodinamika példák - Ideális gáz körfolyamata izobár és adiabatikus állapotváltozásokkal
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
-
 mólnyi ideális gáz az ábrán látható körfolyamatot végzi. A körfolymat két izobár és két adiabata szakaszból áll, amelyeket a
mólnyi ideális gáz az ábrán látható körfolyamatot végzi. A körfolymat két izobár és két adiabata szakaszból áll, amelyeket a 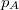 ,
, 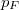 ,
, 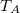 és
és 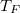 adatok határoznak meg (ez a gőzgép sémája).
adatok határoznak meg (ez a gőzgép sémája).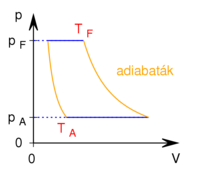
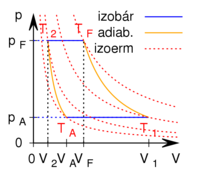
- a) Mekkora a gőzgép hatásfoka?
- b) Hogyan függ a hatásfok attól, hogy hány atomos gázmolekulákkal végezzük a körfolyamatot?
- c) Az adott gépnél és az adott gáznál hogyan növelhető a hatásfok?
Megoldás
a) Hőcsere csak az izobár szakaszokon történik. A hatásfok definíció szerint
![\[ \eta = 1-\frac{|Q_\text{le}|}{Q_\text{fel}}=1-\frac{C_p(T_1-T_A)}{C_p(T_F-T_2)}. \]](/images/math/3/b/4/3b46b62834fbd37656bd4e9681ef4980.png)
Adiabatikus állapotváltozásnál 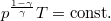 , ezért bevezetve az
, ezért bevezetve az  változót a jelen körfolyamatban
változót a jelen körfolyamatban
![\[ \frac{T_1}{T_F} = \left(\frac{p_A}{p_F}\right)^\frac{1-\gamma}{\gamma} \equiv x \qquad\text{és}\qquad \frac{T_2}{T_A} = \frac{1}{x}. \]](/images/math/8/c/e/8ce181d0eb1746b0ef6588ee85471a4b.png)
Ezt behelyettesítve a hatásfok kifejezésébe
![\[ \eta = 1-\frac{T_Fx-T_A}{T_F-T_A\frac{1}{x}} = 1-x = 1-\left(\frac{p_A}{p_F}\right)^\frac{1-\gamma}{\gamma}. \]](/images/math/0/e/e/0ee5f2832299df491c32975a46274939.png)
b) Tudjuk, hogy 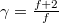 , amiből a fenti kitevő
, amiből a fenti kitevő 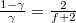 ,
ezt alkalmazva megállapítható, hogy a hatásfok a szabadsági fokok számának csökkentésével nő, hiszen
,
ezt alkalmazva megállapítható, hogy a hatásfok a szabadsági fokok számának csökkentésével nő, hiszen 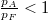 :
:
![\[ \eta = 1-\left(\frac{p_A}{p_F}\right)^\frac{2}{f+2}. \]](/images/math/4/c/3/4c3f64949e0694ca6cfb9a8a33e8557a.png)
c) A nyomásviszony növelésével 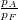 csökkenthető, ezáltal a hatásfok nő.
csökkenthető, ezáltal a hatásfok nő.