Termodinamika példák - Ideális gáz állapotváltozása p-V összefüggéssel
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Termodinamika - Fajhő, Körfolyamatok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Ideális gáz állapotváltozását a
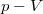 síkon a
síkon a 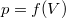 összefüggés írja le.
összefüggés írja le.
- a) Bizonyítsa be, hogy ebben a folyamatban a fajhő térfogatfüggését a összefüggés adja meg!
![\[c(V)=c_V+R\frac{f(V)}{f(V)+V\frac{\mathrm{d}f}{\mathrm{d}V}}\]](/images/math/9/5/f/95f7a48280858181d4b28ca447b3a9d2.png)
- b) Milyen
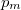 ,
, 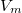 értékpárnál maximális a gáz hőmérséklete, ha az állapotváltozást a
értékpárnál maximális a gáz hőmérséklete, ha az állapotváltozást a 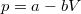 egyenlet adja meg (
egyenlet adja meg ( és
és  ismert pozitív állandók)?
ismert pozitív állandók)?
- a) Bizonyítsa be, hogy ebben a folyamatban a fajhő térfogatfüggését a
Megoldás
a) Egy tetszőleges folyamat során mérhető fajhő meghatározásához annak a közölt hőmennyiséggel megadott 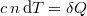 definíciójából kell kiindulnunk, ami pedig az első főtételből számítható:
definíciójából kell kiindulnunk, ami pedig az első főtételből számítható:
![\[ \delta Q = \mathrm{d}U + p\,\mathrm{d}V \]](/images/math/1/6/3/1635c527bc6dbb6f3ab31c4de2e96f72.png)
![\[ c\,n\,\mathrm{d}T = c_V n\,\mathrm{d}T + p\,\mathrm{d}V \]](/images/math/7/d/d/7ddc7315fd5c15ca16d0c250b3c783b4.png)
![\[ c = c_V + \frac{1}{n} \,p \left(\frac{\mathrm{d}V}{\mathrm{d}T}\right)_{\substack{\text{állapot-}\\ \text{változás}}}. \]](/images/math/2/a/2/2a22b715ed9451bfe16c918a2dfaa5a9.png)
A nyomás a 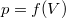 függvénykapcsolattal adott, ezért a fenti, állapotváltozás pályáján vett deriváltat is ezzel kell kifejeznünk. Induljunk ki az ideális gáz állapotegyenletéből (
függvénykapcsolattal adott, ezért a fenti, állapotváltozás pályáján vett deriváltat is ezzel kell kifejeznünk. Induljunk ki az ideális gáz állapotegyenletéből (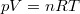 )!
Küszöböljük ki a
)!
Küszöböljük ki a  változót az állapotváltozásra vonatkozó ismereteink segítségével:
változót az állapotváltozásra vonatkozó ismereteink segítségével:
![\[ f(V)V = nRT. \]](/images/math/a/2/5/a257d886f29bfd452df22a506b4d1470.png)
Ebből  csak implicit módon fejezhető ki, ezért az eredeti derivált helyett
csak implicit módon fejezhető ki, ezért az eredeti derivált helyett
![\[ \left(\frac{\mathrm{d}T}{\mathrm{d}V}\right)_{\substack{\text{állapot-}\\ \text{változás}}} = \left[\left(\frac{\mathrm{d}V}{\mathrm{d}T}\right)_{\substack{\text{állapot-}\\ \text{változás}}}\right]^{-1}\]](/images/math/e/f/a/efaae7b045bb32350991dd2a3d0a3cda.png)
értéket számítjuk ki. (Fontos megjegyezni, hogy a deriváltak ilyen kapcsolata akkor és csak akkor áll fenn, ha a deriváltak léteznek, és azonos pályára számítjuk őket.)
![\[ T = \frac{f(V)V}{nR} \qquad \Rightarrow \qquad \left(\frac{\mathrm{d}T}{\mathrm{d}V}\right)_{\substack{\text{állapot-}\\ \text{változás}}} = \frac{1}{nR} \left(\frac{\mathrm{d}f}{\mathrm{d}V}V + f \right). \]](/images/math/1/7/6/17635479706d145b08f5ccef31ef8098.png)
Ezt behelyettesítve a fajhőképletbe
![\[ c = c_V + \frac{f}{n} \frac{nR}{\frac{\mathrm{d}f}{\mathrm{d}V}V+f} \]](/images/math/8/c/2/8c2e37497b158a149c9c2448b5f78440.png)
adódik, amiből már egyenesen következik a feladat állítása.
b) Felhasználjuk a hőmérsékletre az előbb levezetett összefüggést, amibe most beírjuk 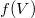 explicit alakját:
explicit alakját:
![\[ T = \frac{(a-bV)V}{nR}. \]](/images/math/e/a/b/eab31ae5a4a1022ecd03f0d5f81ce692.png)
Ennek a kifejezésnek 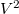 negatív együtthatója miatt maximuma van, ami szélsőértékkereséssel határozható meg:
negatív együtthatója miatt maximuma van, ami szélsőértékkereséssel határozható meg:
![\[ 0 = \left.\frac{\partial T}{\partial V}\right|_{V_m} = \left.\frac{a-2bV}{nR}\right|_{V_m} \qquad \Rightarrow \qquad V_m = \frac{a}{2b}. \]](/images/math/d/8/a/d8a60f80bdf80976fb41d88ec9e303c9.png)
A maximális hőmérséklethez tartozó nyomás pedig
![\[ p_m = f(V_m) = a-\frac{a}{2} = \frac{a}{2}. \]](/images/math/1/9/6/19636dee5cc18b794beb1a56a043e2aa.png)