Termodinamika példák - Carnot-körfolyamat munkája, hatásfoka

Feladat

1. Tekintsünk ideális gázzal végzett Carnot-körfolyamatot.
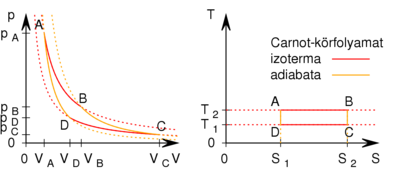
   • a) Ábrázoljuk a Carnot-körfolyamatot 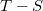$\setbox0\hbox{$T-S$}% \message{//depth:\the\dp0//}% \box0%$ diagramban!
   • b) Mutassuk ki, hogy a körfolyamatban a gáz által végzett munka most is a körfolyamat területével egyenlő!
   • c) Számítsuk ki a fentiek alapján a Carnot-körfolyamat hatásfokát!

Megoldás

a) A hőerőgépet a geometriai negatív körüljárás irányban üzemeltetjük (az ábrának megfelelően). Az 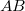$\setbox0\hbox{$AB$}% \message{//depth:\the\dp0//}% \box0%$ szakaszon hőfelvétel, a 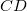$\setbox0\hbox{$CD$}% \message{//depth:\the\dp0//}% \box0%$ szakaszon hőleadás történik.

Általában is elmondható, hogy amikor a folyamat vonala 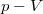$\setbox0\hbox{$p-V$}% \message{//depth:\the\dp0//}% \box0%$ diagramban az adiabatánál kisebb (negatívabb) meredekségű, akkor hőleadás, ellenkező esetben hőfelvétel történik, ezeket a szakaszokat olyan pontok választják el, ahol az adiabata a folyamat vonalához húzott érintő.

b) Az első főtétel alapján 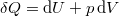$\setbox0\hbox{$ \delta Q = \mathrm{d}U + p\,\mathrm{d}V $}% \message{//depth:\the\dp0//}% \box0%$, ezt a folyamatra integrálva

$\[ \oint \delta Q = \oint \mathrm{d}U + \oint p\,\mathrm{d}V. \]$

Definíció szerint 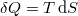$\setbox0\hbox{$\delta Q = T\,\mathrm{d}S$}% \message{//depth:\the\dp0//}% \box0%$. Mivel a körfolyamatban a rendszer eredeti állapotába jut vissza 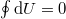$\setbox0\hbox{$\oint \mathrm{d}U=0$}% \message{//depth:\the\dp0//}% \box0%$, azaz

$\[ \oint T\,\mathrm{d}S = \oint p\,\mathrm{d}V. \]$

a körfolyamatban a gáz által végzett munka most is a körfolyamat területével egyenlő, a két diagramban (az ábrának és a konvenciónak megfelelő tengelyirányítással) a körüljárási irány megegyezik.

c) A hatásfokot definíció szerint számítjuk:

$\[ \eta=1-\frac{Q_\text{le}}{Q_\text{fel}}=1-\frac{T_2\Delta S}{T_1\Delta S}=1-\frac{T_2}{T_1}. \]$