Termodinamika példák - Entrópiaváltozás izobár táguláskor
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Entrópia, II. főtétel |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Mennyivel változik meg
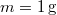 nitrogéngáz entrópiája, ha állandó nyomáson
nitrogéngáz entrópiája, ha állandó nyomáson 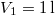 térfogatról
térfogatról 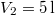 térfogatra expandáltatjuk.
térfogatra expandáltatjuk.
Megoldás
Az entrópiaváltozás definíciója
![\[ \mathrm{d}S = \frac{\delta Q}{T}, \]](/images/math/c/b/d/cbd5cf7c09169ef24d1244b4e66f68f5.png)
amibe helyettesítsük be a közölt hő első főtételből kifejezett
![\[ \delta Q = \mathrm{d}U+p\,\mathrm{d}V \]](/images/math/f/2/1/f2158c0604f29f1f878df0d5c9709b7f.png)
alakját, ahol 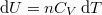 és
és 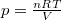 :
:
![\[ \mathrm{d}S= n C_V \frac{\mathrm{d}T}{T} + nR \frac{\mathrm{d}V}{V}. \]](/images/math/6/5/1/651158de62329408881901bb946a3ae9.png)
Kiintegrálva az egyenletet  kezdeti- és
kezdeti- és  végállapot között:
végállapot között:
![\[ S_2 - S_1 = n C_V \ln\frac{T_2}{T_1} + nR \ln\frac{V_2}{V_1}, \]](/images/math/d/f/1/df173414052f078a4bc508e9e42cdf8f.png)
ahol most izotermikusan 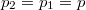 ezért
ezért 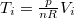 (
(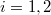 ):
):
![\[ \Delta S = n C_p \ln \frac{V_2}{V_1}, \]](/images/math/0/f/8/0f8c5c16c17844cf1b9d1a87bd9541fb.png)
ahol 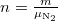 .
A nitrogén kétatomos közel ideális gáz (
.
A nitrogén kétatomos közel ideális gáz (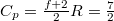 ), móltömege
), móltömege 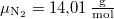 , amikkel
, amikkel 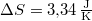 .
.