„Magnetosztatika példák - Tranziens jelenség LR körben” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Megoldás) |
||
| 13. sor: | 13. sor: | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| − | + | Az áramkört modellezhetjük egy sorba kapcsolt ellenállással és tekerccsel. Írjuk fel a hurok-törvényt az áramkörre! A következő differenciál egyenletet kapjuk: | |
$$U = RI + L\dot{I}$$ | $$U = RI + L\dot{I}$$ | ||
| − | + | A kezdeti feltétel pedig a következő: | |
$$I(t = 0) = 0$$ | $$I(t = 0) = 0$$ | ||
Ez egy lineáris elsőrendű differenciál egyenlet, amelyet a változók szétválasztásával oldhatunk meg. | Ez egy lineáris elsőrendű differenciál egyenlet, amelyet a változók szétválasztásával oldhatunk meg. | ||
| 21. sor: | 21. sor: | ||
Ebből a differenciál egyenlet megoldása: | Ebből a differenciál egyenlet megoldása: | ||
$$I\left(t\right) = \frac{U}{R}\left(1-e^{-\frac{R}{L}t}\right)$$ | $$I\left(t\right) = \frac{U}{R}\left(1-e^{-\frac{R}{L}t}\right)$$ | ||
| − | Ebből látszik, hogy az áram maximális értéke: $I_{max} = \frac{U}{R}$, ami érthető, hiszen a stacionárius állapot beállta után a tekercs jelenléte | + | Ebből látszik, hogy az áram maximális értéke: $I_{max} = \frac{U}{R}$, ami érthető, hiszen a stacionárius állapot beállta után a tekercs jelenléte invariáns. Ha ki akarjuk számolni, hogy mikor éri el az áram a maximális értékének $50 \%$-át, akkor a következő egyenletet kell megoldanunk: |
$$1-e^{-\frac{R}{L}t} = 0.5$$ | $$1-e^{-\frac{R}{L}t} = 0.5$$ | ||
Aminek megoldása: | Aminek megoldása: | ||
A lap 2013. szeptember 15., 18:25-kori változata
Feladat
- Egy
induktivitású és 
ellenállású tekercset egy 
elektromotoros erejű telephez kapcsolunk. Mennyi idő alatt éri el az áram az állandósult értékének az 
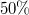-át?
Megoldás
Az áramkört modellezhetjük egy sorba kapcsolt ellenállással és tekerccsel. Írjuk fel a hurok-törvényt az áramkörre! A következő differenciál egyenletet kapjuk:
![\[U = RI + L\dot{I}\]](/images/math/6/1/f/61f65662333a98f63038ead1853d1a96.png)
A kezdeti feltétel pedig a következő:
![\[I(t = 0) = 0\]](/images/math/c/b/1/cb1ecae85437c58916b7dfcc0429e41d.png)
Ez egy lineáris elsőrendű differenciál egyenlet, amelyet a változók szétválasztásával oldhatunk meg.
![\[\int_0^I\frac{d\tilde{I}}{\frac{U}{L}-\frac{R}{L}\tilde{I}} = \int_0^t d\tilde{t}\]](/images/math/e/f/7/ef743c09c9342a76af67ea085cb040ed.png)
Ebből a differenciál egyenlet megoldása:
![\[I\left(t\right) = \frac{U}{R}\left(1-e^{-\frac{R}{L}t}\right)\]](/images/math/1/4/f/14f2ab223ef700e0d8284bbe19bb7d04.png)
Ebből látszik, hogy az áram maximális értéke: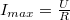 
, ami érthető, hiszen a stacionárius állapot beállta után a tekercs jelenléte invariáns. Ha ki akarjuk számolni, hogy mikor éri el az áram a maximális értékének 
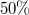-át, akkor a következő egyenletet kell megoldanunk:
![\[1-e^{-\frac{R}{L}t} = 0.5\]](/images/math/c/2/3/c23aa7d77a294c435bfa47d799f0ff15.png)
Aminek megoldása:
![\[t = -\frac{L}{R}\ln\left(0.5\right)\]](/images/math/4/8/1/481d84668ebc507feb6a27b633dd9ffc.png)
