„Magnetosztatika példák - Eltolási áram síkkondenzátorban” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
(→Megoldás) |
||
| 13. sor: | 13. sor: | ||
== Megoldás == | == Megoldás == | ||
<wlatex> | <wlatex> | ||
| − | a, Mivel $\omega$ állandó, ezért a $D$ | + | a, Mivel $\omega$ állandó, ezért a $D$ elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis: |
$$\frac{\partial D}{\partial t} = 0$$ | $$\frac{\partial D}{\partial t} = 0$$ | ||
b, Ha kondenzátor lemezei között az $U$ feszültség állandó, akkor: | b, Ha kondenzátor lemezei között az $U$ feszültség állandó, akkor: | ||
$U = E\cdot d = E\cdot u\cdot t = \frac{D}{\epsilon_0}\cdot u\cdot t$ | $U = E\cdot d = E\cdot u\cdot t = \frac{D}{\epsilon_0}\cdot u\cdot t$ | ||
| − | Amiből: | + | Amiből az elektomos eltolás nagysága: |
$$D = \frac{\epsilon_0 U}{ut}$$ | $$D = \frac{\epsilon_0 U}{ut}$$ | ||
Az etolási áram pedig: | Az etolási áram pedig: | ||
A lap 2013. szeptember 15., 19:34-kori változata
Feladat
- Határozzuk meg, mekkora az eltolási áram egy olyan síkkondenzátor esetén, amelynek lemezei egymással párhuzamosak maradnak, miközben
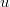 sebességgel távolodnak egymástól, ha
sebességgel távolodnak egymástól, ha
a) az töltéssűrűség állandó
töltéssűrűség állandó
b) a lemezek közötti feszültség állandó.
Megoldás
a, Mivel  állandó, ezért a
állandó, ezért a  elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis:
elektromos eltolás nagysága is állandó a kondenzátor lemezei között. Az eltolási áram értéke tehát zérus. Vagyis:
![\[\frac{\partial D}{\partial t} = 0\]](/images/math/1/c/c/1cc2bd06331a5f4b5abd0bb327a36516.png)
b, Ha kondenzátor lemezei között az  feszültség állandó, akkor:
feszültség állandó, akkor:
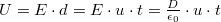 Amiből az elektomos eltolás nagysága:
Amiből az elektomos eltolás nagysága:
![\[D = \frac{\epsilon_0 U}{ut}\]](/images/math/0/9/b/09b52911ae0d981b405d57a99440edf7.png)
Az etolási áram pedig:
![\[\frac{\partial D}{\partial t} = -\frac{U \epsilon_0}{ut^2}\]](/images/math/0/b/4/0b4c599dac950846ccaeceb05815b655.png)